- Programming and Data Science Club
- First meeting: Tuesday, 5:30 PM Bailey 101
- Solutions available online through our
“Exercises” page
- Complete exam 2
- Problem set 10 (set algebra)
- Section 6.2
- Progress check 6.6: defining f and g as functions from ℤ5 to
ℤ5 by f(x) = x4 (mod 5) and g(x) = x5 (mod 5), are either f or
g equal to the identity function on ℤ5?
- f = g if and only if
- Domain of f = domain of g
- Codomains are equal
- For all x in dom(f) f(x) = g(x)
- ℤn = { 0, 1, …, n-1 } = integers mod n
- Identity function, I(x) = x
- Iℤ5 : ℤ5 → ℤ5
- Iℤ5(0) = 0, Iℤ5(1) = 1, …, Iℤ5(4) = 4
- Check
- Domains equal (ℤ5)
- Codomains equal (ℤ5)
- f(2) = 24 (mod 5) = 1
- So f ≠ Iℤ5
- g(2) = 25 (mod 5) = 2
- So f ≠ g
- Iℤ5(0) = 0 = g(0),
Iℤ5(1) = 1 = g(1),
Iℤ5(3) = 3 = g(3),
Iℤ5(4) = 4 = g(4)
- But how did I know 35 (mod 5) = 3? Just need one’s digit of
35
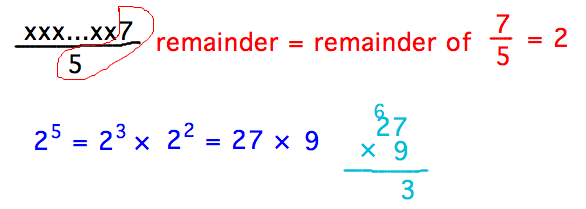
- So g = Iℤ5
- But how did I know 35 (mod 5) = 3? Just need one’s digit of
35
- f = g if and only if
- Recalling the idea from Friday that a function can be represented as a set of
ordered pairs, is Sundstrom’s definition of function equality equivalent to
the sets of ordered pairs being equal?
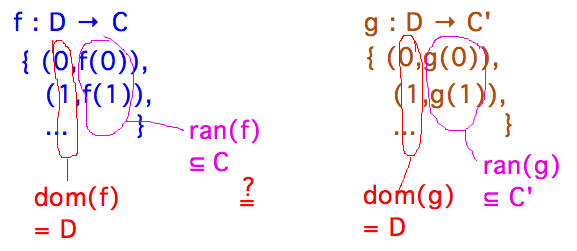
- Function equality is almost set equality except for codomains
- Some important classes of function
- Read section 6.3