Conservative Vector Fields

Return to Course Outline

Previous Lecture

Misc

End of semester announcements.

SOFIs

I do read them, and the written comments are particularly helpful for informing how I teach this course next time, so please fill one out for this course.

Thanks to 3 of you have already done them!

Deadlines

Any grading should be finished by May 14 (the last day of finals). If you need a significant extension beyond then, talk to me by May 14 about an incomplete.

Also give me extra credit write-ups by May 14.

Questions?

Problem set question 4b about increasing speed of water as it gets closer to a drain?

Since the vector field in question gives velocity, and speed is the magnitude of velocity, I suggest looking at the magnitude of the vectors. I’ll be happy with an answer that shows that this magnitude is something that “obviously” gets larger as distance from the origin gets smaller, you don’t have to formally prove that part. So, for example...

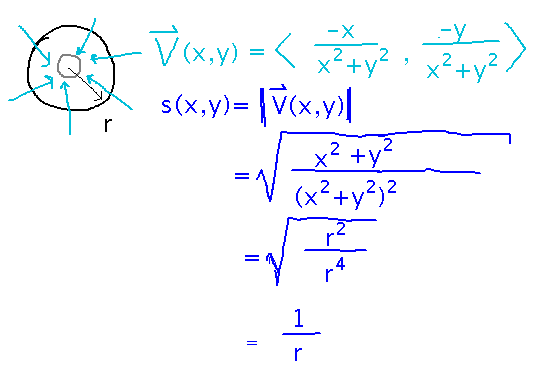
Conservative Vector Fields

I seem to remember that the first time we used the term “vector field” in this course was when we talked about gradients, and realized that gradients are vector fields. So they make good source of line integral problems. For example...

Let f(x,y) = xy, so ∇f = ⟨ y, x ⟩, which we can call vector field F(x,y). Suppose we have a path r(t)= ⟨ t, t² ⟩ for -1 ≤ t ≤ 1. Find the line integral (parallel to r) of F along this path.

Use the standard method, i.e., express the integral as F(r(t)) · r’(t), multiply out the dot product, and integrate:

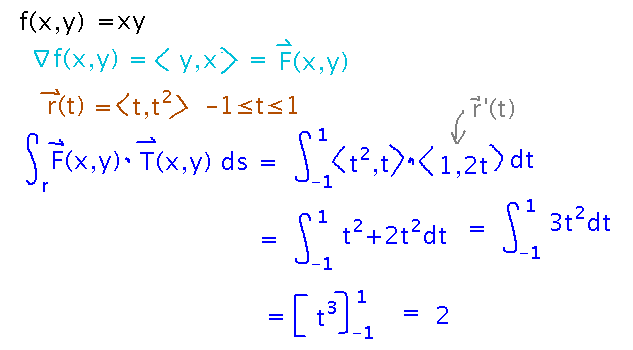
What’s f(r(1)) - f(r(-1)) (i.e., the difference between f values at the beginning and end of the path)?

Oddly, it comes out the same as the line integral. Something interesting is going on....

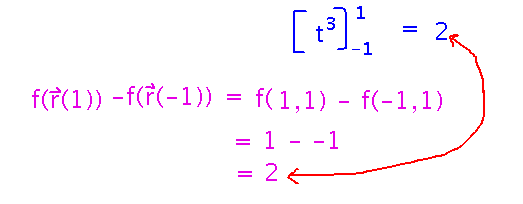
What’s going on is that this vector field is a gradient, also known as a “gradient field” or a “conservative field.” Conservative vector fields always support the simple integration trick analogous to the Fundamental Theorem of Calculus that I demonstrated above. They are also common and important in physics (among other applications), where they model forces that conserve energy.

For example, find the gradient vector field for f(x,y,z) = 3x + 2y - z sin x + xyz. This just requires finding ∇f, as you did a month or so ago:

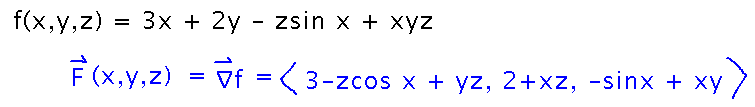
Gradient fields have another interesting property that helps you tell when a vector field isn’t a gradient: If you think of the components of the gradient as derivatives of f, and thus the components’ derivatives as second derivatives, Clairaut’s Theorem tells you that some of those derivatives have to be equal. This is sometimes called the “cross-partials property.” For example, for a 2-dimensional field:

You can also see that a 3-dimensional version holds for the example gradient field above:

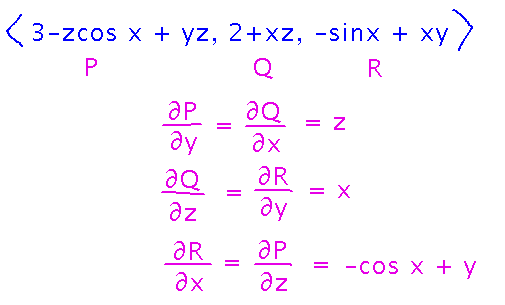
Next

Conservative vector fields and potential functions

Please read section 15.3

Next Lecture