Misc
End of semester announcements.
SOFIs
I do read them, and the written comments are particularly helpful for informing how I teach this course next time, so please fill one out for this course.
2 of you already have! Thank you!
Deadlines
Any grading should be finished by May 14 (the last day of finals). If you need a significant extension beyond then, talk to me by May 14 about an incomplete.
Also give me extra credit write-ups by May 14.
Questions?
Flux and Circulation
“Flux” and “Circulation” subsections of section 15.2.
Key Ideas or Questions
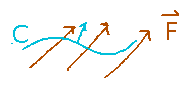
Flux is roughly the flow of a vector field across a curve.
Circulation is the flow of the field along the curve.
Examples
I occasionally do amateur beer brewing. Part of that process involves circulating hot water through a bag of grains to give the beer its flavor. I do this by heating water in a big kettle, while moving the bag in a circle inside that kettle. Although I move the bag through nominally stationary water, the water’s interaction with the bag is the same as if the water moved and the bag were stationary. So it can be modeled something like this, where V is the velocity field for the water relative to the bag:
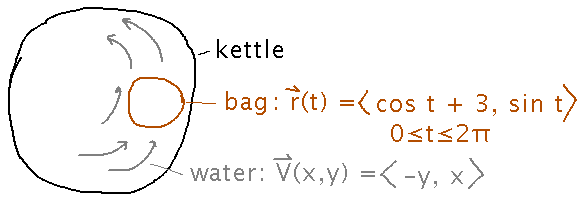
I want a large flux of water through the bag, to pick up the largest amount of flavor. What is the flux through the bag?
Start by writing the integral in the “V(r(t)) · n(t)” form:
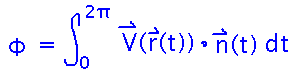
Then fill in the vectors, multiply out the dot product, and evaluate the resulting single-variable integral:
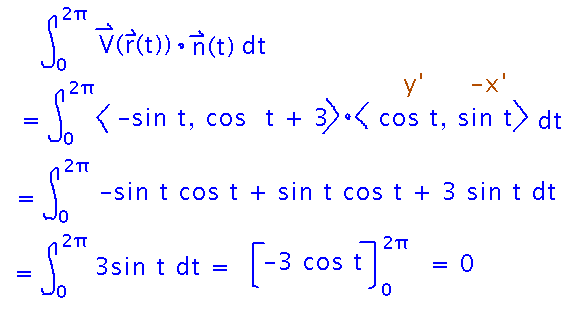
A flux of 0 looks really bad if I want a large amount of water flowing through my grains. What’s wrong, and what would be a better flux calculation?
The problem is that the flux calculation captures all flow across the bag, both in and out. Presumably flow in balances flow out. So calculating flux across just the upper part of the bag (for flow out) would give me a better sense of what I want to know. Flux across part of the curve is easy to calculate now, because it uses the same vectors and integrands, just with different bounds:
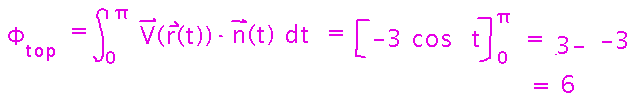
How about the circulation of water around the bag?
This is really just the old vector line integral parallel to a path that we’ve seen before:
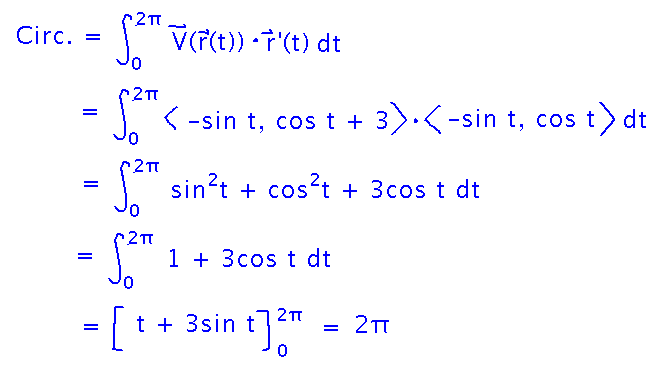
Next
The last variation on vector fields.
No reading yet.