Misc
End of semester announcements.
SOFIs
SOFIs are under way. You should have gotten an email about how to participate.
Please fill one out for this course. I do read them, and the written comments are particularly helpful for informing how I teach this course next time.
Deadlines
Any grading extensions should be finished by May 14. If you need a significant extension beyond then, talk to me about an incomplete.
Also give me extra credit write-ups by May 14 (the last day of finals).
Questions?
How many more problem sets will there be? One more, graded during finals week (since we don’t have a final as such).
Whirlpool
Last class we suggested V(x,y,z) = 〈 -y, x, -1/(x+y) 〉 as a vector field that simulated the velocity of water swirling down a drain. This suggestion wasn’t very satisfying when plotted, partly because the vectors approach infinite length in multiple places, and partly because it therefore exercises an awkwardness in Mathematica’s VectorPlot3D function.
Suggestions for another field? How about using the actual distance of point (x,y) from the origin to control how strongly downward the field points?
Plotting this with Mathematica yields:
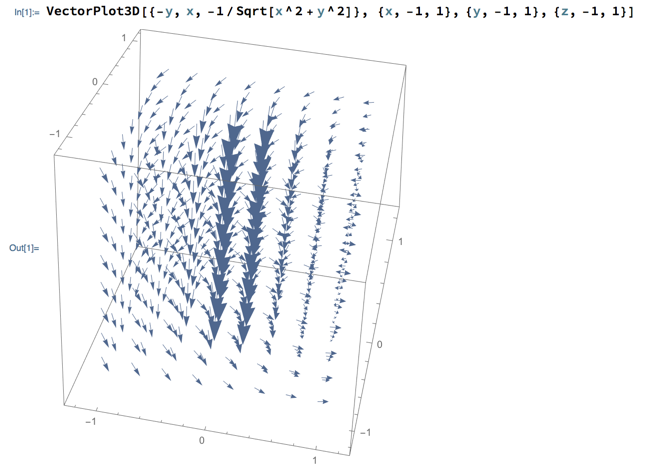
You can download the Mathematica notebook here.
Line Integrals in Vector Fields
“Vector Line Integrals” in section 15.2.
Key Idea(s) or Questions
Why do these line integrals depend on a unit tangent vector? Because they are really integrals of 1 way vector fields can interact with a curve: integrals of the vectors’ projections onto the path . Projections onto a path are dot products with the tangent to that path. (There’s another source of vector line integrals too, integrals of projections perpendicular to the path. We’ll talk about that shortly.)
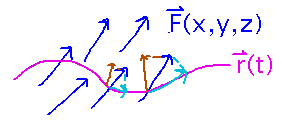
Line integrals of projections parallel to the path have a calculational formula that is easier to work with than the “F · T” form that motivates them. This formula integrates F(r(t)) · r’(t).
Example
Integrate F(x,y) = ⟨ 4-y, -10 ⟩ along the path r(t) = ⟨ t, t2 ⟩ from t = 0 to t = 2. This would, for example, be the work required to push a 1 kilogram cart up a track described by r(t), if you have a tailwind exerting 4-y Newtons of force to help you.
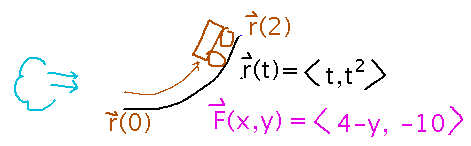
Start by expressing work as the integral along the cart’s path of force exerted parallel to that path.
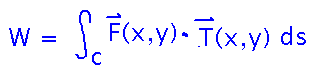
This is the classic line-integral-parallel-to-path form. To derive the calculational form from it, recall that T = r’/|r’|. Once we take the dot product we’re integrating a scalar, and scalar line integrals multiply the integrand by |r’| -- this cancels out the division by |r’| in T, leaving F(r(t)) · r’(t).
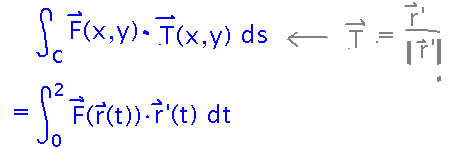
From here, substitute the appropriate expressions for x and y in terms of t into F, carry out the dot product, and integrate:
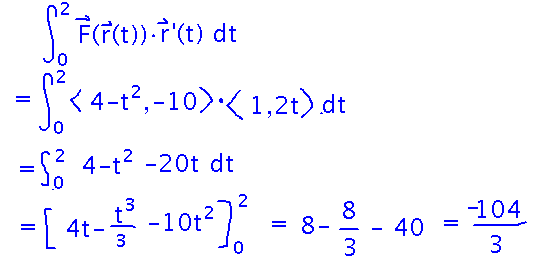
Alternative Form
Integrands of the form F(r(t)) · r’(t) are also sometimes written as P(x,y) dx + Q(x,y) dy. How does this work? It’s the dot product of the components of F with the components of r’.
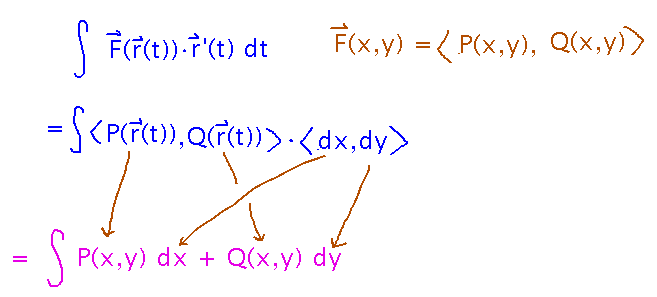
Next
Flux and circulation: two other applications of vector line integrals.
Please read “Flux” and “Circulation” in section 15.2.