SUNY Geneseo Department of Mathematics

Mass and Moment in 3 Dimensions

Monday, April 20 - Friday, April 3

Math 223 01
Spring 2020
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Questions?

A 3-Dimensional Mass and Moment Example

Geneseo (Genne) Jones, archeologist-adventurer, plunderer of antiquities, and general embodiment of Hollywood stereotypes, has found the lost Temple of Turmoil and its Pyramid of Peril. The Pyramid is held upside-down on its tip by a rope. At the other end of the rope is an immense treasure. The problem is that the pyramid is unbalanced, so that if Genne unties the treasure, the pyramid will fall over and awaken the giant Guardian Viper. Fortunately, Genne has wedges to stick under two sides of the pyramid to keep it from falling -- but which sides? Upon studying the Pyramid, Genne sees that it is labeled with a handy coordinate system, in which it occupies the region between the origin and the planes z = 1, x = z, x = -z, y = z, and y = -z. Moreover, a manufacturer’s tag glued to the Pyramid helpfully adds that its density is given by the function ρ(x,y,z) = ez - xy2.

Geneseo Jones trying to figure out how to support upside down pyramid

Last time we decided to find the center of mass, and then look at the signs of its x and y coordinates.

So now we need to actually find the center of mass, with Mathematica.

But before we can use Mathematica, we need to figure out what integrals to evaluate with it. The integral for mass from density is just like it’s 2 dimensional version, i.e., the integral of density, except integrated over 3 dimensions instead of 2. The relevant moments are slightly different, because they are moments relative to coordinate planes rather than axes (e.g., Mxy is the moment relative to the xy plane), but they are defined using the same idea of integrating density times distance from the (in this case) plane:

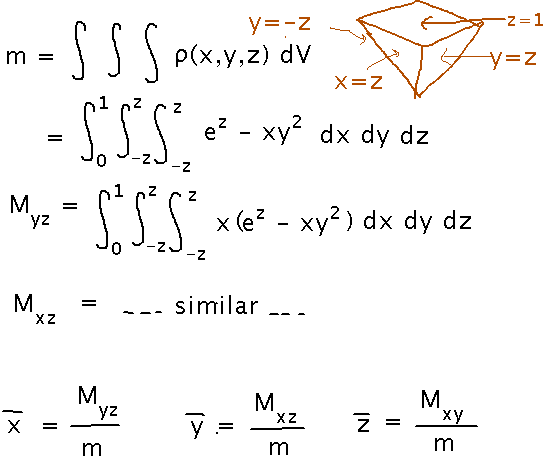
Mass as integral over volume of density, moments as integrals of density times distance from plane

Now integrate these in Mathematica. The results are in this notebook.

Introduction to Scalar Line Integrals

From “Scalar Line Integrals” in section 15.2.

Key Idea(s)

Another kind of multivariable integral, but along an arbitrary curve, rather than over some area or along an axis.

Line integrals are defined as Riemann sums of the function value times differential distance along the curve, but that’s a hard form to calculate with. So there’s another formula for calculating line integrals:

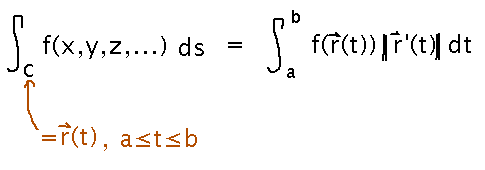
Integral of f with respect to arc length is integral of f of r of t times magnitude of r prime with respect to t

By setting the function to the constant 1, you get the usual formula for arc length:

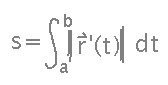
Arc length equals integral of magnitude of r prime

You saw this formula back when we studied vector-valued functions, but line integrals give you a way to understand it as a special case of something more general.

Next

Examples of scalar line integrals. (We started an example at the end of today’s class, but it turns out that as an introductory example, it’s badly broken -- i.e., messy enough to integrate that the mess would distract from the ideas it’s supposed to introduce -- so I think we’re better off starting over with a better one.)

Remember that “next” is Thursday, April 23 (Wednesday is virtual GREAT Day; go take a look at the GREAT Day exhibits, available at https://www.geneseo.edu/great_day and worth a bit of extra credit).

Next Lecture