Mass and Moment

Return to Course Outline

Previous Lecture

Questions?

Mass and Moment

Section 14.7 (and particularly “Center of Mass in Two Dimensions”)

Key Idea(s)

Mass is the integral of density over as many dimensions you have.

Moment (in 2D space) is relative to an axis, and is the integral of density times the variable not associated with that axis (i.e., the “other variable”).

Two-Dimensional Example

Imagine a thin plate (lamina) bounded by the x axis and the curve y = 1 - x². The density of this plate is given by ρ(x,y) = x²y. Find the total mass and center of mass. I recommend using Mathematica to evaluate the integrals and arithmetic.

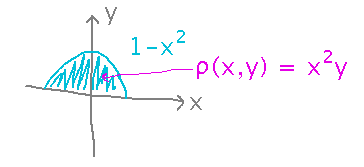
Before getting to Mathematica, we have to set up the integrals. They follow the formula’s summarized under “Key Ideas”:

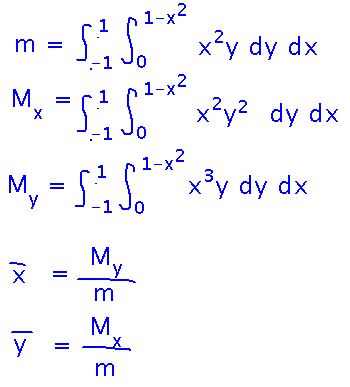
Now evaluate these with Mathematica. This notebook has the result.

Three Dimensions

Can you generalize the formulas to 3 dimensions?

Yes: the generalization for mass is the triple integral of density over 3 dimensions.

There are 2 ways to generalize moment:

• One is based on distance from an axis, e.g., M_z = √(x²+y²) m.
• The other, which is what our book discusses when it gets to 3-dimensional moments, is based on distance from a plane, e.g., M_xy = z m.

Center of mass in 3 dimensions is based on M_xy, M_yz, and M_xz.

Example — Geneseo Jones and the Pyramid of Peril: Geneseo (Genne) Jones, archeologist-adventurer and general embodiment of Hollywood stereotypes, has found the lost Temple of Turmoil and its Pyramid of Peril. The Pyramid is held upside-down on its tip by a rope. At the other end of the rope is an immense treasure. The problem is that the pyramid is unbalanced, so that if Genne unties the treasure, the pyramid will fall over and awaken the giant Guardian Viper. Fortunately, Genne has a wedge to stick under one side of the pyramid to keep it from falling -- if they can just figure out which side to put it under. Upon studying the Pyramid, Genne sees that it is labeled with a handy coordinate system, in which it occupies the region between the origin and the planes z = 1, x = z, x = -z, y = z, and y = -z. Moreover, a manufacturer’s tag glued to the Pyramid helpfully adds that its density is given by the function ρ(x,y,z) = e^z - xy².

Which side should Jones put the wedge under?

A good basic idea is to find the center of mass, and then look at the signs of its x and y coordinates. If the x coordinate is, say, less than 0, put the wedge on the negative x side of the pyramid; if the x coordinate of the center of mass is positive, put the wedge on the positive x side of the pyramid. Treat the y coordinate similarly.

We’ll work out the coordinates (with Mathematica again) at the start of Monday’s class.

Next

After the “Pyramid of Peril” example...

Another variation on multivariable integration (and transition to vector fields): what if you wanted to integrate over a line or curve rather than a region?

Please read “Scalar Line Integrals” in section 15.2.

Next Lecture