Polar Integral Applications

Return to Course Outline

Previous Lecture

Misc

Reminder about yesterday’s GREAT Day announcement. Its key points are

• An opportunity for extra credit if you visit any one math-related exhibit and write a short description of and reaction to it. “Description” really just means identify the topic; “reaction” is the usual few sentences or short paragraph.
• No class meeting next Wednesday, April 22.

Questions?

An Application of Polar Integration

I think (but I expect everyone is too wise to listen to me on this) that Geneseo’s new library should be a mostly rectangular building, but with a big circular tower at the center of the front. The only reason for the tower is so that a glassed-in study area can wrap around the front half of it. The study area should have a curved wall/roof whose height above floor level is given by

h = √(4-r²)

where r is the distance from the center of the tower, in units that are totally made up, for the sole purpose of making the arithmetic in this problem easier. Whatever those units are, the tower proper has a radius of 1 unit, so the study area extends from r = 1 out to r = 2.

What is the volume of this study area?

The basic calculation is just integrating the height of the region over it’s floor area:

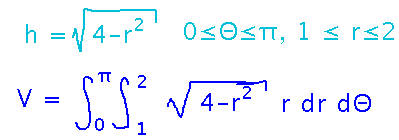
Start evaluating the integral with a u-substitution that conveniently takes advantage of the “r dr” part of the polar integral. From there, evaluation is mostly a matter of doing the arithmetic and algebra. There are a couple of alternative places you could do some of the simplifications though.

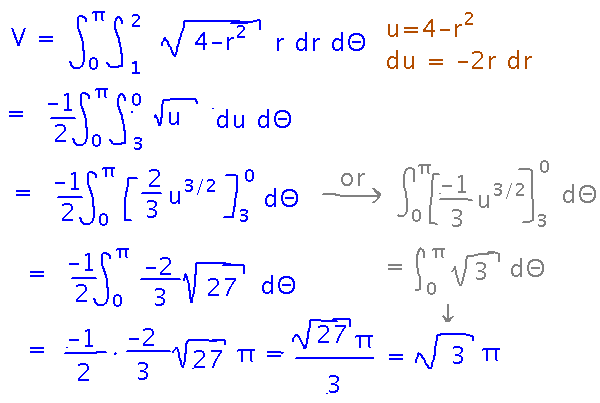
Next

Applications of multiple integrals to mass, moment, etc.

The basic idea is to calculate certain physical quantities of three-dimensional objects whose density varies with position. In particular, we’re interested in calculating total mass (M), and moments with respect to various axes or planes (e.g., M_x, moment with respect to the x axis, or M_yz, moment with respect to the yz plane). With mass and moment, we can also calculate centers of mass:

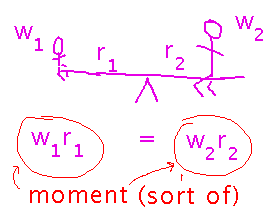
What is moment? Intuitively, think of it as a measure of how much a mass tilts something out of balance. For instance, you probably figured out in elementary school that if a big person and a little person want to balance on a seesaw, the big person should sit closer to the center than the small person -- you want a situation in which the products of weight times distance from the center for the two people are equal. That product is intuitively what moment is about, except that moment is properly defined by distance and mass, not distance and weight.

Read “Center of Mass in Two Dimensions” in section 14.7 of the textbook.

Next Lecture