SUNY Geneseo Department of Mathematics
Thursday, April 9
Math 223 01
Spring 2020
Prof. Doug Baldwin
Yesterday we saw that you can compute the area of a plane region as the integral over that region of the constant function f(x,y) = 1.
For example, use a double integral to find the area of the rectangle -1 ≤ x ≤ 1, 2 ≤ y ≤ 6. Notice that this rectangle is 2 units wide and 4 units high, so the area ought to come out to be 8 square units.
Integrating 1 over the rectangle leads directly to the expected answer. But notice 2 ways to evaluate the integral: the first based on realizing that 1 can be treated as a product of two functions, one f(x) = 1 and the other f(y) = 1, and so the integral can be evaluated as a product of single variable integrals; the second based on standard iterated integration:
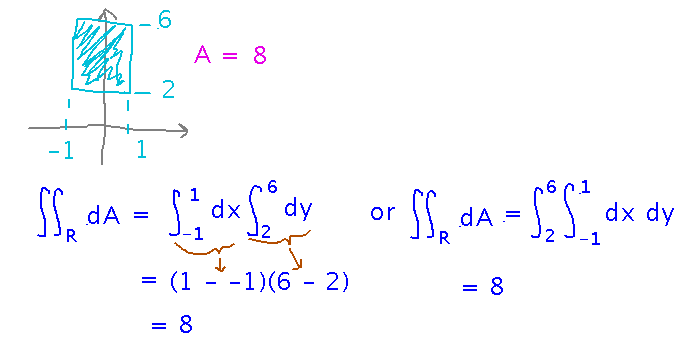
How about the area of the region 0 ≤ x ≤ 2, 0 ≤ y ≤ 2x - x2 (also as a double integral, I suspect you already know how to do it as a single-variable integral)?
Use ideas related to integrating over non-rectangular regions to integrate 1 over a region whose x coordinates range from 0 to 2, and whose y coordinates range from 0 to 2x - x2:
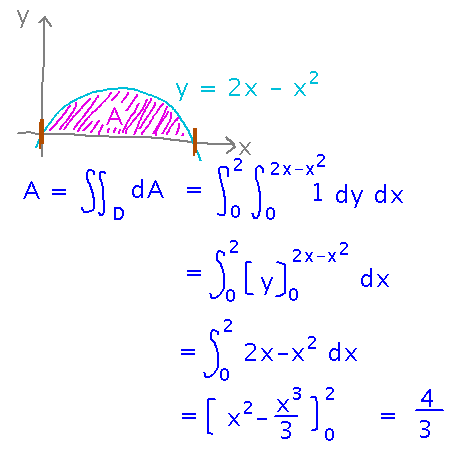
This, of course, involved an example of...
Section 14.3 in the textbook (except for “Improper Double Integrals”).
Think of the regions as having constants as the bounds in one dimension, and functions of that variable as the bounds in the other dimension.
Type I vs type II: y as a function of x (type I) vs. x as a function of y (type II).
Thus we have integrals with functions as bounds, but you plug those bounds into antiderivatives just as you would do with constant bounds.
What is the volume of the region above the triangle bounded by the lines x = 1, y = 0, and y = x and below the surface z = x2 + y2 (in other words, integrate x2 + y2 over the given triangle)?
Express the triangle as a type I region, i.e., x ranges from 0 to 1 while y ranges from 0 to x. Then integrate:
More integration over general regions.
No new reading.