Questions?
Multiple Integrals over Rectangular Regions
The first 3 subsections in section 14.2 of the textbook.
Order of Integration
Monday we started looking at the integral of x e2xy over the region 0 ≤ x ≤ ln 3, 0 ≤ y ≤ 1. We found that evaluating the integral was likely to be very different depending on whether we integrated first with respect to y or with respect to x.
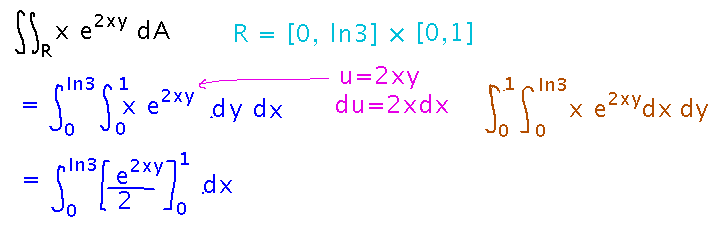
How did finishing these (or at least one of them) go? Everyone seems to have chosen to integrate with respect to y first (good choice!). Evaluating that integral involves lots of work, but the work is mostly straightforward:
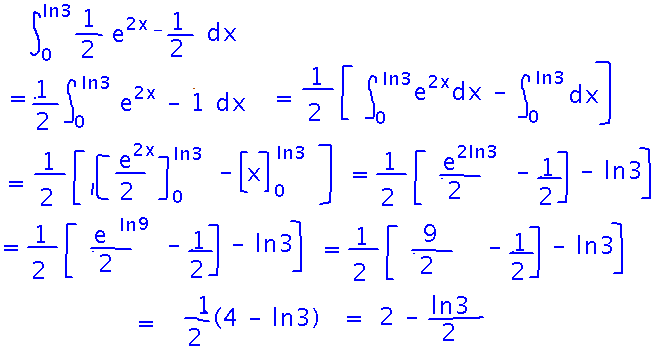
More than 2 Variables
What do you think the integral over R = [0,1] × [0,2] × [0,3] of xyz is?
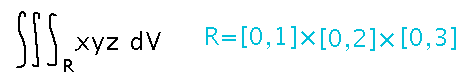
3-variable integrals are conceptually no different from 2-variable ones; similar laws apply. In this case, using the property that says an integral of a product of terms each involving a single variable can be broken into a product of integrals seems quickest:
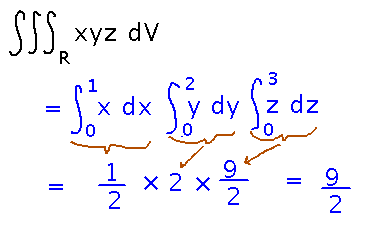
An Application
What is the volume of the region between the rectangle [0,2] × [0,3] in the xy plane and the surface z = x2 + y + 1?
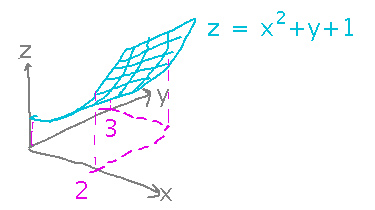
Applications to volumes under a surface come straight from the definition of a double integral as such a volume. So just integrate z over the xy region given...
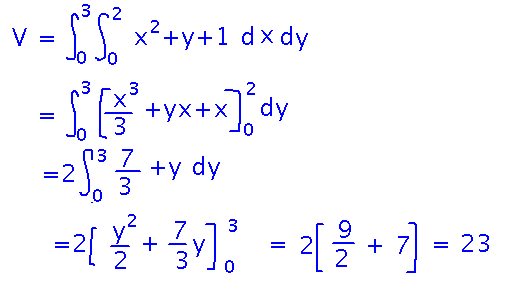
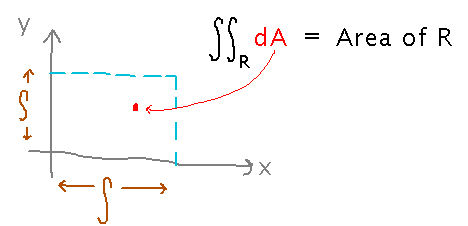
Application to Area
Can you calculate the area of a region as a double integral? (Since the only regions we can integrate over right now are rectangles, using double integrals to find their areas is likely to be overkill. But if we eventually figure out how to evaluate integrals over non-rectangular regions it might be more interesting.)
In fact you can, building on the idea that a double integral is a sum over infinitesimally small areas. Simply summing those areas, i.e., integrating just “1 dA” produces the area of the region:
Next
An example of area as a double integral.
Then start integrating over non-rectangular regions.
Read section 14.3 up to but not including “Improper Double Integrals.”