SUNY Geneseo Department of Mathematics
Wednesday, April 1
Math 223 01
Spring 2020
Prof. Doug Baldwin
Why does the book’s example 13.7.3, part a, seem to ignore the critical point it found?
Because that’s a mistake in the example. The minimum is 17, which occurs only at the critical point (3,1).
You don’t need to give units in your answer to question 4 in problem set 10 (about pressure, volume, and temperature), although they aren’t that hard to work out if you want to.
“Absolute Maxima and Minima” in section 13.7 of the book.
Finding absolute extreme values of a function on some region extends Fermat’s Theorem (that extremes appear at critical points) to say that the extreme values in a closed, bounded, region appear either at critical points or on the boundary of the region.
Find the absolute minimum and maximum of z = x2 + y2 in the xy triangle with vertices (-1,0), (1,1), and (1,-1).
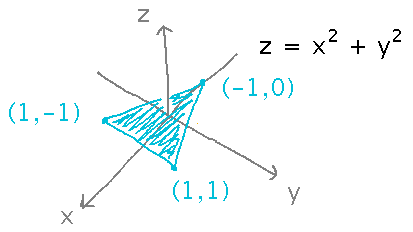
First, find any critical points in the region:
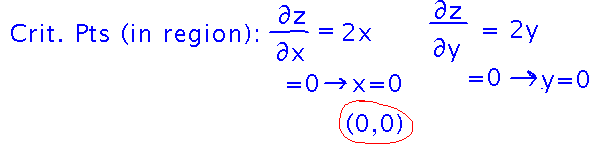
Then find any local minima and maxima along the boundary of the region. Treat each side of the boundary separately. You can either parameterize the lines along the boundary, as done in the textbook, or find equations for y in terms of x along each line -- this may be simpler, since it encourages you to use slope/intercept calculations to find the equations (although those equations are essentially the same as you’d get using the book’s approach):
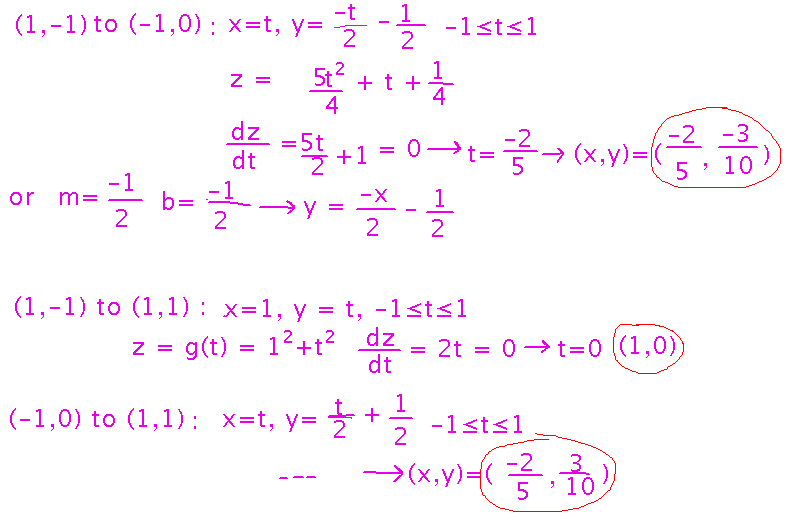
Now we have 1 critical point, 3 extremes along boundary edges, and the 3 corners of the region. We need to evaluate z at all 7 of these points and find the smallest and largest values. Try doing that between now and tomorrow’s class. We’ll summarize the results and/or answer questions in class, then start talking about...
Constrained optimization and Lagrange multipliers.
In other words, solving problems that require finding a minimum or maximum value of a function, but subject to constraints on its inputs. For example, maximize x2 - 4x + 4 + y2 subject to the constraint that x and y lie on the circle x2 + y2 = 1.
Read section 13.8.