Misc
Online Office Hours
Hoping to capture some of the “office hours are any time from 8:00 to 5:00 when I’m not busy with something else” philosophy, I will monitor the Google Hangout at https://meet.google.com/boo-wyaj-hcr from 8:00 to 5:00, when I’m not busy with something else.
Simply clicking on the link in any browser should connect you.
You can also dial in on a phone by calling 914-893-5826 and entering PIN 135 452 070#. That seems functionally the same as making a voice phone call.
I may not get an on-screen notification when people join though, so say something when you get to the hangout, and give me a minute to switch to that window and turn on my microphone.
Other Things from Feedback Surveys
Slow down the pace of problem sets. Yes.
Keep doing “face-to-face” grading. But don’t require it, or synchronous class attendance, because it can be hard for people with poor internet connections. Agreed. Don’t feel you have to attend synchronous class meetings, you can use the recordings or Canvas notes instead, and won’t be penalized for doing so. I want some sort of real-time conversation with you during grading, but that can be a phone call about solutions submitted by email or something rather than a video chat — let me know what you need!
Be very clear about what to read for each class. Yes.
Keep using “class” time to practice problems. Yes.
Relax the “doing what I expect earns 8 out of 10 points” standard. Unfortunately, I still believe this is a good way to encourage you into habits of rising above expectations, and that it remains reasonable to ask even with remote learning and grading.
Math Learning Center
The Math Learning Center is open online.
But only to help 100- and 200-level courses (e.g., you), and only by appointment.
VPN Hint
Geneseo’s “virtual private network,” or VPN, is a piece of software for your computer that makes it look as if your computer is physically on the Geneseo network even when it isn’t. We don’t use that for this course, but some of you may need it for other courses (e.g., if you use Matlab or certain other software gotten through Geneseo, the license may require you to be on the College network). The following was distributed to math majors who might be having trouble with the VPN for Windows, and since some of you aren’t math majors, here it is in case it’s helpful:
“If you are a Windows user and your Geneseo VPN gives you an error that says: ’The network connection between your computer and the VPN server could not be established because the remote servers is not responding. [...]’, remove the VPN from your settings and then install the Cisco AnyConnect app from the Microsoft store. Once you’ve done that, go back to your Windows settings and add a new VPN connection.
- VPN provider: AnyConnect
- Connection name: Geneseo VPN
- Server name or address: asa.geneseo.edu
- If the option to remember your sign-in info is there. leave the box checked.
Save the new connection and then try connecting to it. It should go through without any issues.”
Questions?
The notation “fxx(x,y)fyy(x,y)...” means regular multiplication in the textbook.
Extreme Values
Section 13.7 in the textbook, and our online discussion of extreme values.
Key Points
Local minima and maxima must occur at critical points, i.e., points where all of the function’s partial derivatives are 0 or undefined.
There is a second derivative test for telling minima from maxima from saddle points.
Local Extrema Example
Find the critical points of f(x,y) = x3/3 - x + xy2.
Find the partial derivatives, set them equal to 0, and solve for x and y. In this case, one of the derivatives tells you that either x = 0 or y = 0; the other derivative then lets you find values for the other variable in each of those cases:
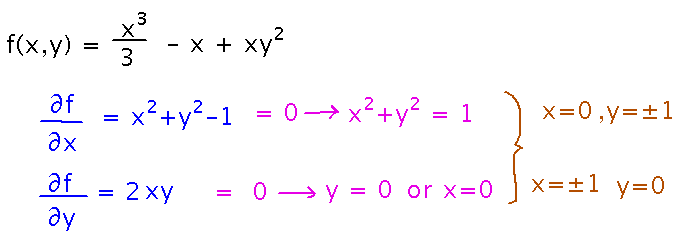
So there are 4 critical points: (0,-1), (0,1), (-1,0), and (1,0).
Classify those critical points as local minima, maxima, or saddle points.
Use the second derivative test. In the case where there’s a minimum or maximum, that test uses the second derivative with respect to x to tell which -- why is the derivative with respect to x special? It isn’t really. The test is looking at the concavity of the function, and once you know there’s a minimum or maximum, the concavity will be the same in both the x and y directions. You could just as well use the second derivative with respect to y, the choice of x is arbitrary.
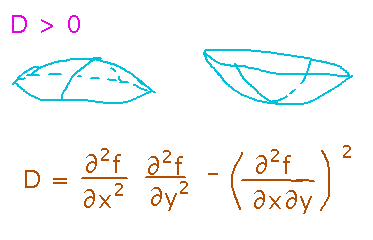
Using the second derivative test on the given function begins by finding the second derivatives, and putting them together according to the discriminant formula:
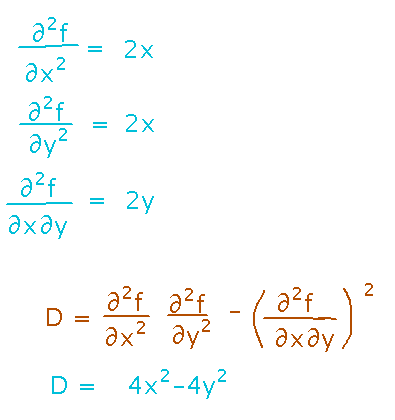
Then plug each critical point into the discriminant (and maybe also into the second derivative with respect to x) to classify the points:
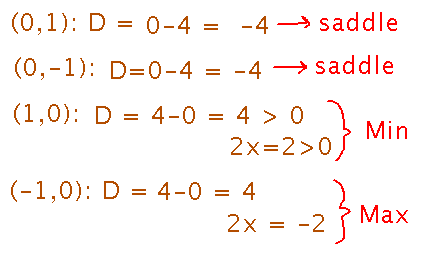
Next
Absolute extreme values.
No new reading. But review “Absolute Maxima and Minima” in section 13.7 if you want.