The Chain Rule

Return to Course Outline

Previous Lecture

Questions?

The Chain Rule for Partial Derivatives

“Chain Rules for One or Two Independent Variables” and “The Generalized Chain Rule” in section 13.5.

Key Point(s)

When a multivariable function is a composition of other functions (i.e., each variable is actually calculated as a function of one or more other variables), the derivative of that function with respect to the ultimate independent variables is a sum of products of derivatives.

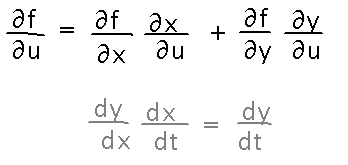
(The difference between “d” and “∂” notation for derivatives: use “d” when there is only one variable to differentiate with respect to, “∂” when there are several variables and you’re indicating which one to use.)

There is a consistent pattern to the products and sum, although it’s hard to describe in words. Tree diagrams capture it visually.

Examples

One Variable

Suppose z = x² + y² - 2x + 2y + 2, x = cos t, y = sin t. Find dz/dt.

Start applying the “sum of products of derivatives” idea by writing out all the partial derivatives z has. Then multiply each one by the derivative of the corresponding variable with respect to t, and add the resulting products:

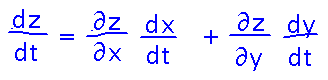
Now calculate the various derivatives you need:

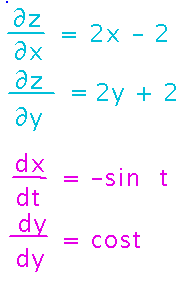
And finally plug them into the sum of products. Write the final result in terms of t, since that’s the variable the desired derivative is in terms of.

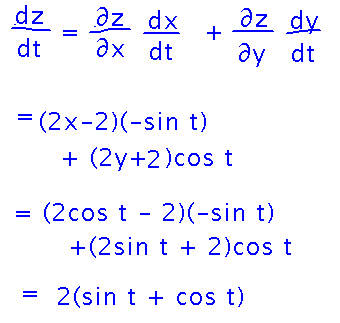
Check the result by writing z as a function of t and differentiating.

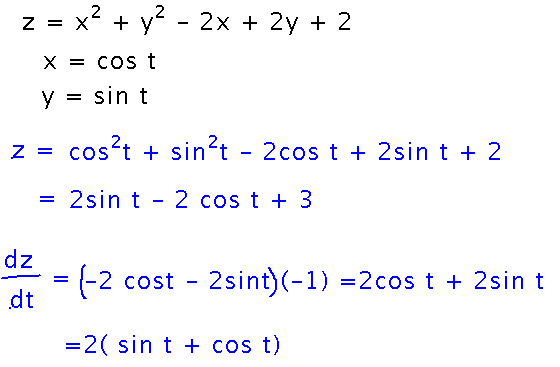
Notice that this is always possible with the multivariable chain rule, i.e., the only time the chain rule directly gives you a way to differentiate things you couldn’t differentiate without it is in the single-variable case. But the multivariable chain rule is extremely useful as a tool in proving other things about partial derivatives.

Two Variables

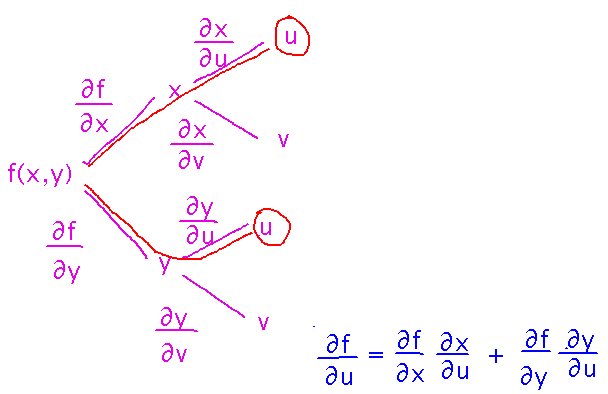
Suppose f(x,y) = e^xy - ln xy, x(u,v) = 2u²v², y(u,v) = u/v.

Draw a tree diagram showing the formula for ∂f/∂u.

The tree diagram has branches for each input to each function. Each branch is labeled with the derivative of the function with respect to the variable. The ends of branches are labeled with variables; if those variables are computed by functions, they have branches too. The derivative of the original function with respect to any independent variable is the sum of the products along each path leading to that variable of the derivatives along that path:

Next

Online discussion about local minima and maxima of multivariable functions.

Complete the first round of discussion by Thursday evening, and the whole thing by Sunday, as stated in the discussion.

After break: directional derivatives.

Read “Directional Derivatives” in section 13.6.

Next Lecture