SUNY Geneseo Department of Mathematics

Tangent Planes and Linear Approximation

Monday, March 9

Math 223 01
Spring 2020
Prof. Doug Baldwin

Questions?

The proof of the tangent plane equation refers to lines/vectors parallel to the xz and yz planes. Why those planes?

Because that’s what partial derivatives give you easily: the derivative with respect to x shows how z changes as x changes and y doesn’t, so gives you the slope of a tangent line parallel to the xz plane. The derivative with respect to y shows how z changes as y changes and x doesn’t.

A surface, tangent lines representing partial derivatives with respect to x and y are parallel to x z and y z planes

Tangent Planes and Linear Approximation

Section 13.4 in the textbook.

Key Points

The equation for a tangent plane.

The equation for linear approximation (which is really the tangent plane equation).

“Tangent plane” is the set of all tangent lines at a point.

Tangent Planes

Let g(x,y) be the “egg carton” function g(x,y) = sin x cos y:

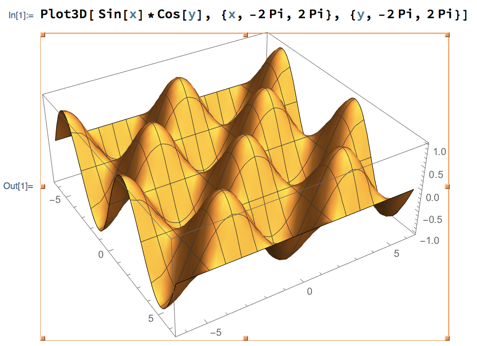
A surface of alternating peaks and dips, like an egg carton

Find an equation for the tangent plane to g(x,y) at (π/2,0). Find the derivatives and plug them, along with g(π/2,0), into the tangent plane formula:

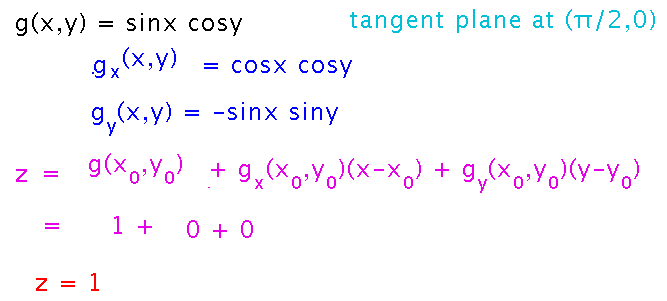
Egg carton function and its derivatives evaluated at point pi over 2, 0 gives tangent z equals 1

Having done that work, you can reuse it to find a more interesting tangent plane, e.g., at (π/4,π/4):

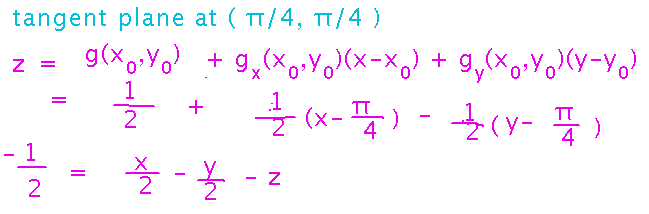
Plugging x equals pi over 4 and y equals pi over 4 into egg carton tangent equation

This one can at least be put into a form that looks like the typical plane equations from a month ago.

Linear Approximation

Consider the function that gives you the length of the diagonal of a rectangle in terms of the rectangle’s width and height:

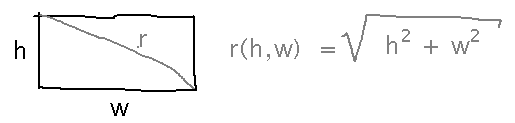
Diagonal has length r of h and w equals square root of h squared plus w squared

Estimate how long the diagonal is when h = 4.05 and w = 2.9. This is a pain to calculate precisely because of the square root, but easy to calculate for h = 4 and w = 3. Using that and the linear approximation formula gives...

Linear approximation of diagonal near h equals 4, w equals 3

Wednesday: video class meeting via Blackboard Collaborate at our usual time (1:30). But you can do it from anywhere you like, and feel free to do it in small groups with one computer rather than everyone having their own computer.

The subject will be the chain rule for partial derivatives. Read “Chain Rules for One or Two Independent Variables” and “The Generalized Chain Rule” in section 13.5.

For Thursday and Friday: watch for a Canvas-based discussion on extreme values of multivariable functions, or possibly implicit differentiation. More on this Wednesday.

Next Lecture