SUNY Geneseo Department of Mathematics

Introduction to Limits of Multivariable Functions

Monday, March 2

Math 223 01
Spring 2020
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Misc

Differential equations experiment is still looking for participants.

It’s a chance to...

This is the last week of the experiment. Drop in at Sturges 106

or schedule an individual time

Questions?

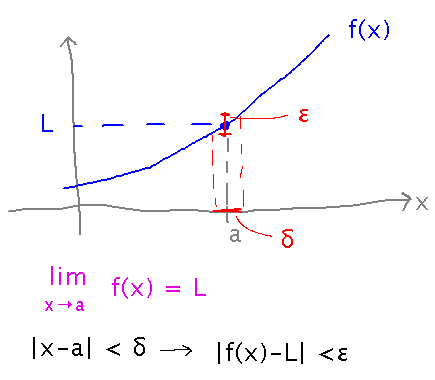
Definition of Limit?

The beginning of this section alludes to a formal definition of the limit of a single-variable function that captures the idea that the limit of f(x) as x approaches a is L means that getting x very close to a gets f very close to L, and in fact no matter how close to L you want to get, you can get close enough to a to do it.

Graph of f of x stays within epsilon of L as long as x stays within delta of a

Limits that Don’t Exist

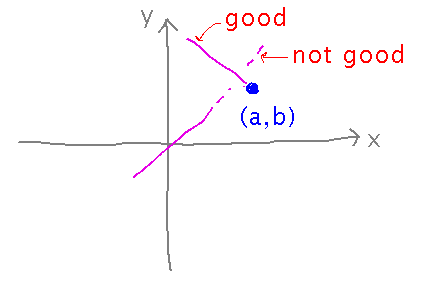
How did book’s author know to use the various paths chosen in Example 13.2.2 (showing that limits don’t exist)?

Some of it is a matter of doing what’s easy and seeing if it helps, e.g., setting one variable equal to the value it’s approaching and letting only the other vary.

Some is also a matter of experience, e.g., knowing that considering approaches along different straight lines often helps show that a limit doesn’t exist.

In all cases, be careful you’re using paths that really do go through the point the limit approaches.

Good path goes through point a, b; bad path doesn't

Limits of Multivariable Functions

Section 13.2.

Key Ideas

Limit laws for 1-variable functions extend to any number of variables. So do techniques for finding limits.

Finding Limits

Find...

lim(x,y)→(1,2) (x+y) / (y2-2x)

Just plug x = 1, y = 2 into the function, as permitted by limit laws:

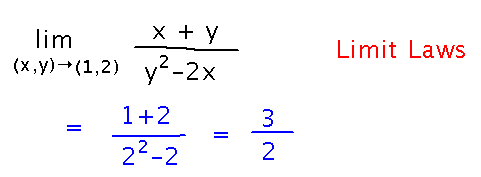
Plug 1 and 2 in for x and y to get limit, per limit laws.

lim(x,y)→(2,2) (xy-y2) / (y2-x2)

Plugging in x = 2, y = 2 yields 0/0, so use subtler techniques. Factoring works, much as it would with a single-variable limit:

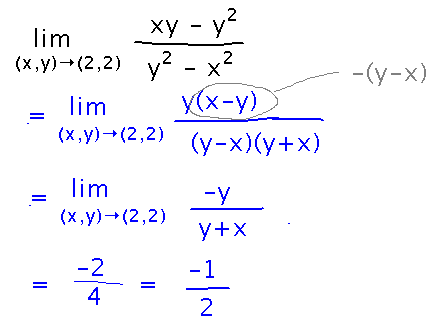
Factoring and canceling denominator lets you plug in x and y values

lim(x,y,z)→(1,4,-2) x(y-z2) / (√y+z)

Again, you can’t just plug x = 1, y = 4, z = -2 into the function. Cleverer factoring, or multiplying by the conjugate, works to get rid of the 0/0 here.

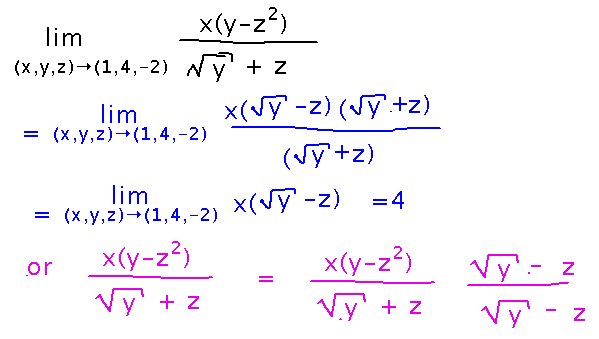
Factoring numerator, or multiplying denominator and numerator by conjugate, simplifies limit

Notice that this limit involved 3 variables. The number of variables doesn’t really affect how you find limits.

Formal Definition

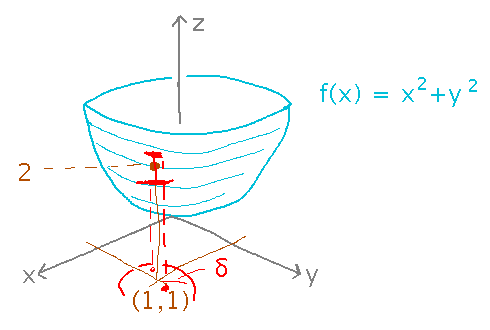
Sketch a picture of what it means that lim(x,y)→(1,1) x2+y2 = 2

Much as in the single-variable case where there’s always a δ interval around a that keeps f(x) within an ε tolerance of L, there’s a δ circle around (1,1) that keeps x2+y2 within an ε tolerance of 2:

Function is within epsilon of 2 as long as x and y are in radius delta circle around point 1, 1

Next

Finish limits of multivariable functions, notably limits that don’t exist.

Continuity of multivariable functions.

No new reading, but review the parts of section 13.2 on limits that don’t exist and continuity.

Next Lecture