SUNY Geneseo Department of Mathematics
Wednesday, February 26
Math 223 01
Spring 2020
Prof. Doug Baldwin
Hour exam 1 is tomorrow (Feb. 27).
Covers material since the beginning of the semester (e.g., 3D coordinates, lines/planes/surfaces, vectors, vector-valued functions, their derivatives and integrals, etc.)
4 short-answer questions (one with 2 parts), similar to mid-difficulty questions from problem sets.
You’ll have the whole class period.
Open book, notes, calculator, computer as a reference or calculator. But closed person.
What direction does the principal unit normal, N, point in?
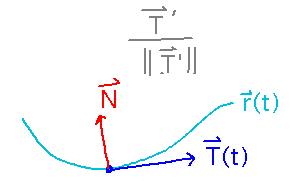
Because the unit normal points in the same direction as the derivative of (i.e., rate of change of) the unit tangent vector, it must point in the direction the curve is turning.
Curvature problems are long and complicated enough that using a tool such a Mathematica to do some of the work for you and keep track of it is helpful.
The “Waterslide of Doom” is a proposed slide that follows the curve r(t) = 〈 cos(4t), sin(4t), 10 - t2 〉. How sharply will it curve?
See this notebook for the calculations, along with commentary.
Things didn’t go as smoothly in class as they do in the notebook linked above. It turns out that the solution to the problems in class was to use a hand-simplified expression for the magnitude of the derivative of the slide throughout. (In class we used that expression in some places, and Mathematica’s unsimplified one in others.) The moral here is to watch what Mathematica (or similar tools) are doing, and try to help them if they seem to miss something you can do.
Defining your own functions ( f[t_] := ....)and variables x= ... or x :=....
(After exam)
Start talking about multivariable functions, i.e., functions that depend on more than 1 input (in contrast to vector-valued functions which in some sense have more than 1 output).
Read section 13.1.