SUNY Geneseo Department of Mathematics
Thursday, February 6
Math 223 01
Spring 2020
Prof. Doug Baldwin
Section 11.4.
There’s a formula for the cross product (and various mnemonics for it, and you can look it up when you need it; if you use it often you’ll memorize it simply through use).
Results in a vector perpendicular to u and v.
Also has other applications, e.g., torque, certain area calculations.
Find 〈 2, 1, -4 〉 × 〈 -3, 1, 6 〉(similar to Example 11.4.1)
⟨ (6- -4), -(12-12), (2- -3) ⟩ = ⟨ 10, 0, 5 ⟩ = 10i + 5k
You could also write the operand vectors in standard unit vector form, then take advantage of the fact that cross product distributes over vector addition and subtraction to rewrite the product as a sum of cross products involving only standard unit vectors, and finally take advantage of the fact that there are simple rules for the cross products of the standard unit vectors (e.g., i×j = k, etc.)
(2i + j -4k)×(-3i+j+6k) ...
This is a lot of work at first, but avoids needing to memorize or evaluate the general formula for cross product.
Last class we had a video game character with “right” vector r = ⟨ 2, 1, 0 ⟩ and “forward” vector f = ⟨ -1, 2, 0 ⟩. Find an “up” vector for this character.
From the right-hand rule, r × f gives a vector that points in the “up” direction. Then just use the cross product formula:
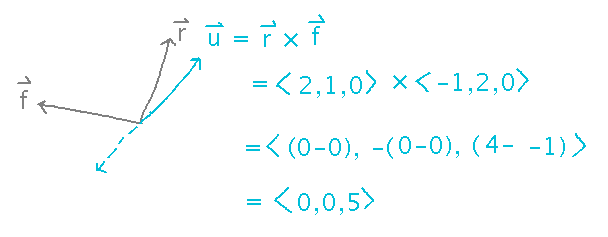
Find a vector perpendicular to (aka a “normal” to) the plane containing points (2,0,0), (1,1,0), and (0,0,1). Make the normal point away from the origin.
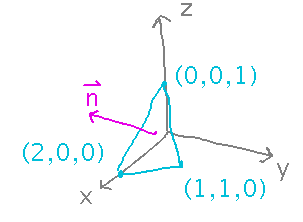
If you had 2 vectors parallel to the plane of the triangle, you could use their cross product (in the right order) as the normal. To find those vectors, notice that the vectors between any 2 of the points are “in” the triangle (though properly speaking vectors don’t have positions, just directions and magnitudes).
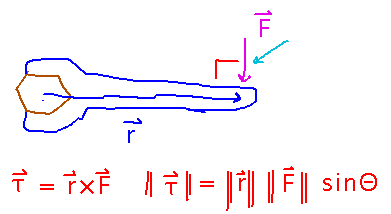
Why is it best to push a wrench perpendicular to its handle?
Because torque (the amount a force makes something want to turn) is a cross product of a force vector with a radius vector, and the magnitude of a cross product depends on the sine of the angle between the vectors. 90 degrees has the largest possible sine.
Equations for general lines.
Read “Equations for a Line in Space,” “Distance between a Point and a Line,” “Relationships between Lines” in section 11.5.