Misc
Colloquia
First: “Elasticity Imaging Inverse Problem of Locating Cancerous Tumors”
Prof. Akhtar Khan, RIT School of Mathematical Science
Friday, February 7, 3:30-4:30, Newton 203.
Second: “Mathematical Modeling in Virology”
Dr. Jonathan Forde, Dept. of Mathematics and Computer Science, Hobart and William Smith Colleges
Monday, February 10, 4:00 - 5:00 PM, Newton 202
This is also a preview of REU opportunities at Hobart and William Smith
Extra credit for going to either or both and writing roughly a paragraph on connections you make between your interests and the talk, or other reflection/reaction to it. But please not just a summary of the content. Paragraphs are “due” by the final exam time.
PRISM Party
Welcome back to the spring semester.
Pizza, people, etc.
Thursday, February 6, 4:00, Fraser lounge.
PRISM is also looking for people interested in serving on their executive committee. Find an officer at the party, or email prism@geneseo.edu for more information or to express interest.
Questions?
Projections (Especially for Computer Graphics)
In a first-person video game there are 2 sets of axes: a “global coordinate system” in which the game world is defined, and a “viewer coordinate system” in which the player actually sees things.
The viewer coordinate system is defined by direction vectors (axes) relevant to the viewer: typically “right,” “forward” (or “backward”), and “up”.
To figure out how the viewer sees things, you need to project them from the global coordinate system onto the viewer’s axes (i.e., direction vectors).
For example, suppose a viewer’s right vector is 〈 2, 1, 0 〉 and their forward vector is ⟨ -1, 2, 0 ⟩. How do they see an object moving with velocity ⟨ 0, -1, 0 ⟩?

Start by figuring out just the scalar components of velocity projected onto the right and forward vectors, i.e., how fast the viewer sees this object moving left/right and forward/backward:
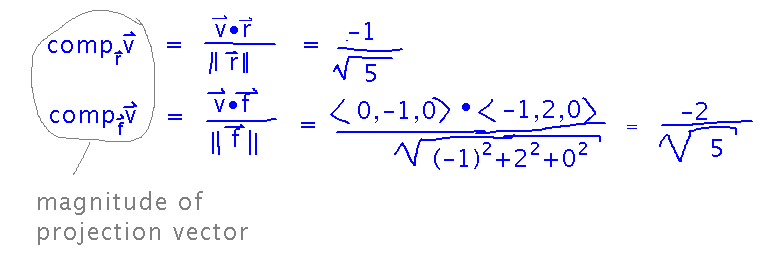
The actual vectors for those components of velocity, i.e., speed and an exact direction, are also interesting:
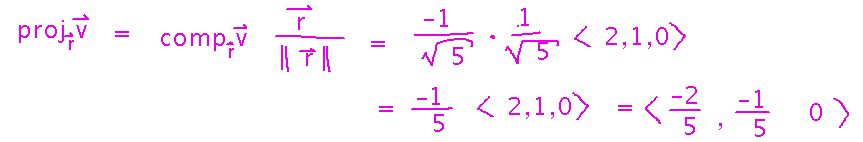
Cross Products
Section 11.4.
Key Ideas
Cross product formula?
I remember it as a pattern of multiplications across the vectors subtracted from each other, and alternating the sign of the whole difference. For each component of the product, you do this cross-multiplication with the other elements of the multiplicands.
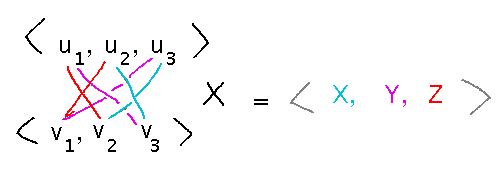
Cross product of u and v is perpendicular to both u and v.
Next
More thorough study of the cross product.
Finish reading section 11.4.