Questions?
Projection and Force
What is with the discussion of projections and force?
The key idea is “projecting” one vector onto another, i.e., determining what part of the first vector is parallel to the second. This has lots of applications to forces acting on bodies that can’t move in exactly the direction the force is pushing. For example, an “ice gremlin” pushing down on a skater’s shoulders exerts some force parallel to the ice that makes her move, but some of the gremlin’s force is directed into the ice and has no effect:

Or gravity pulling down on a block on an inclined plane can be thought of as having a component parallel to the incline that makes the block slide, and a component perpendicular to the plane that does nothing:
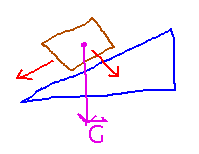
In both cases, you can multiply the force parallel to the direction of motion by the distance moved to get the “work” done, i.e., the energy added to the moving body.
The general math of these situations is a vector v being projected onto a vector u:
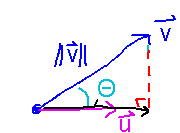
The magnitude of the projected vector is the magnitude of v times cosΘ, where Θ is the angle between v and u. Thanks to the relationship between cosines and dot products ( u • v = ||u|| ||v|| cosΘ), the magnitude of the projection has a simple formula in terms of dot product:
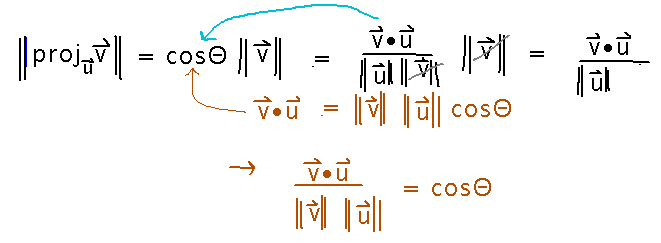
Angle
How do dot products relate to angles?
Via the formula for cosine introduced above.
See how via an example: what is the angle between ⟨ 1, 1/4, -2 ⟩ and ⟨ 2, 2, 1 ⟩?
Take the expression for cosΘ derived above one step further to get Θ as an inverse cosine:
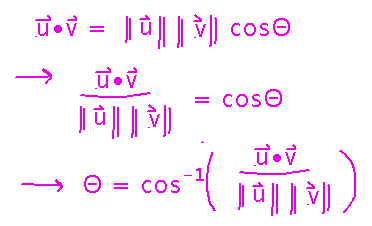
Now plug the actual vectors from the problem into this formula and calculate:

Dot Products
Section 11.3.
Key Ideas
(Most of these came out implicitly during the questions above.)
Formula for the dot product of 2 vectors.
Connection between dot product and angle.
Two non-zero vectors have a zero dot product if and only if they are perpendicular.
Connection between dot product and projection.
More about Angle
Are ⟨ 4, 0, -3 ⟩ and ⟨ 1, 2, 1 ⟩ perpendicular? No, because their dot product isn’t 0. (The angle between perpendicular vectors has to be 90 degrees, aka π/2 radians, which has a cosine of 0. The only way the dot product based formula for cosΘ can be 0 is if the dot product of u and v is 0.)

Could you make the vectors perpendicular? Yes. For example, either change ⟨ 4, 0, -3 ⟩ to ⟨ 4, 0, -4 ⟩, or ⟨ 1, 2, 1 ⟩ to ⟨ 3,0,-4 ⟩.
Next
More about projections.
Then cross products.
Start looking at section 11.4.