Misc
Final Exam
Tuesday, May 8, 12:00 noon to 3:20 PM, in our regular classroom.
Comprehensive, but with an emphasis on material since the 2nd hour exam (e.g., directional derivatives, gradients, Lagrange multipliers, multiple integrals & their applications, line integrals, vector fields, etc.)
Designed to be 2 to 2 1/2 times as long as the hour exams, but you have 4 times as much time.
Rules and format otherwise similar to hour exams, particularly including the open-references rule.
I’ll provide a sample from a past semester.
I’ll bring donuts and cider.
SOFIs
3 filled out as of this morning - thank you!
They are useful to me in improving courses for the future, and you get 1 printer dollar / SOFI. So please fill them out.
Green’s Theorem
Flux Form
Check that Green’s theorem and the standard line integral for flux give the same answer for the flux of F(x,y) = 〈 -y, x 〉around the semicircle of radius 1 above the origin.
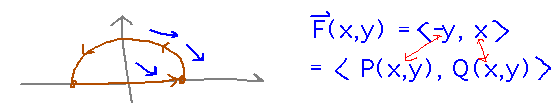
To find the flux value via Green’s theorem, evaluate the double integral in the flux form over the semicircle:
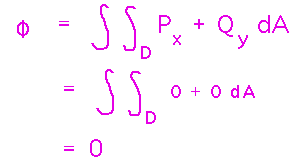
To find the flux via a line integral, we need parametric forms for the curve and bottom of the semicircle, and the corresponding “n” functions.
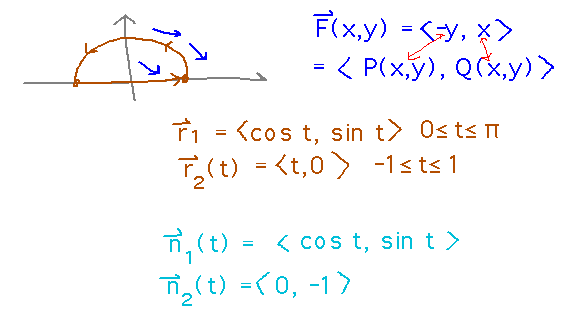
Now we can evaluate the line integrals over each part of the semicircle to get the flux:
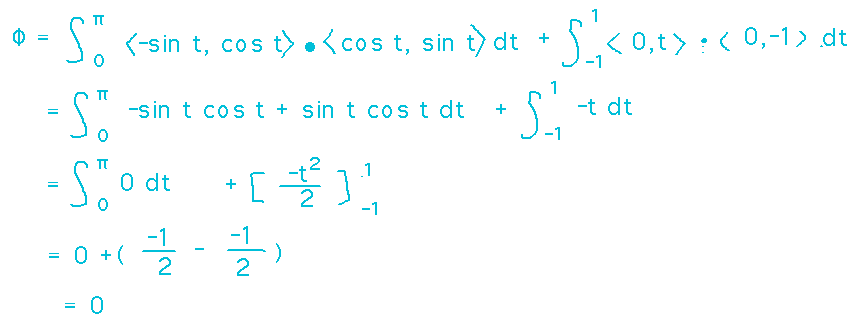
An Equivalence
Consider
![]()
This can be read as either a circulation line integral or a flux line integral, thus demonstrating an equivalence between those line integrals. What are the line integrals?
The “obvious” origin of this double integral is from the circulation form of Green’s theorem, i.e., it corresponds to a circulation line integral for F(x,y) = 〈 P(x,y), Q(x,y) 〉. But it could also come from the flux form of Green’s theorem, for a field whose x component was Q and whose y component was -P, i.e., G(x,y)= 〈 Q(x,y), -P(x,y) 〉.
Since these two line integrals both equal the same double integral, there’s an equivalence between the circulation of one field and the flux of the other, i.e., the circulation of field〈 P(x,y), Q(x,y) 〉 around any path equals the flux of field 〈 Q(x,y), -P(x,y) 〉across that same path.
Next
Calculating area via Green’s theorem.
Source-free fields and stream functions.