Misc
Colloquium
“Particle Swarm Optimization”
Prof. Ahmad Almomani, SUNY Geneseo
Thursday, April 26, 2:30 PM
Newton 203
Extra credit as usual for roughly a paragraph on your reactions or connections to the talk.
Final Exam
Tuesday, May 8, 12:00 noon to 3:20 PM, in our regular classroom.
Comprehensive, but with an emphasis on material since the 2nd hour exam (e.g., directional derivatives, gradients, Lagrange multipliers, multiple integrals & their applications, line integrals, vector fields, etc.)
Designed to be 2 to 2 1/2 times as long as the hour exams, but you have 4 times as much time.
Rules and format otherwise similar to hour exams, particularly including the open-references rule.
I’ll provide a sample from a past semester.
I’ll bring donuts and cider.
Review Session?
Would you like one, probably on study day (Wednesday May 2)?
If so, what time and for how long?
Conclusion: yes, one would be helpful, for approximately an hour. I’ll let you know what I can schedule.
SOFIs
Now under way; you should have gotten an email about filling them out online.
I will see results (anonymously and after the end of the semester), and they are useful to me in improving courses for the future. And you get 1 printer dollar / SOFI. So please fill them out.
Questions?
Conservative Vector Fields
Potential Functions
Use the book’s method to find a potential function for F(x,y,z) = 〈 2xy - sin z, x2 + z, y - x cos z 〉.
Identifying the components of F as P, Q, and R as the book does, the first step is to integrate P with respect to x. Since P is the derivative of f (the potential function) with respect to x, this integral should be the potential function.
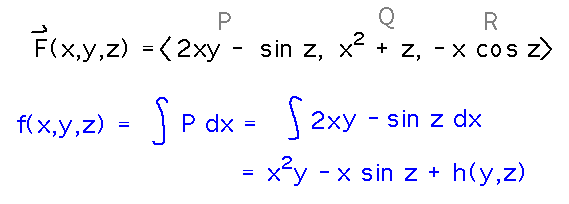
Unfortunately, the “constant” of integration in this integral could be any function of y and/or z. To get more specific about that function, try differentiating f as known so far with respect to some other variable (say, y) and comparing the result to what we know it must be from the Q component of F.
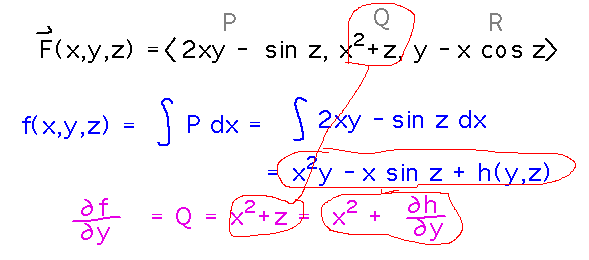
This gives us a value for the derivative of the unknown function, which we can integrate to get a better version of f.
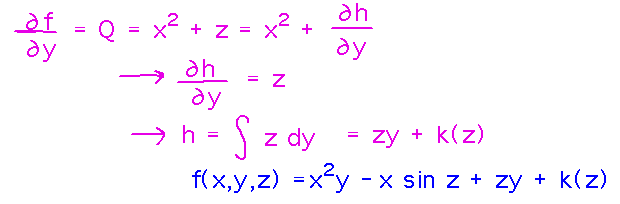
But this better version still has an unknown function in it, this time depending only on z. So repeat the process again, this time looking at the derivative of f with respect to z:
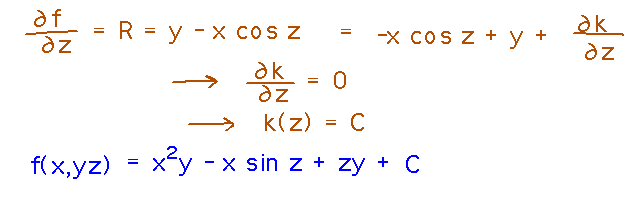
This finally gives us the most accurate potential function we can get.
The Cross Partial Test
A Negative Example
Show that F(x,y,z) = 〈 -y, x, z 〉is not conservative
Once again, identify the components of F as P, Q, and R. Then the cross partial test says to compare certain derivatives of P, Q, and R. As soon as we find that one of the specified pairs of derivatives isn’t equal we know F isn’t conservative and can stop.
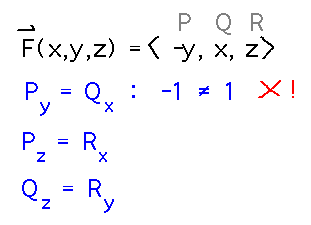
A Positive Example
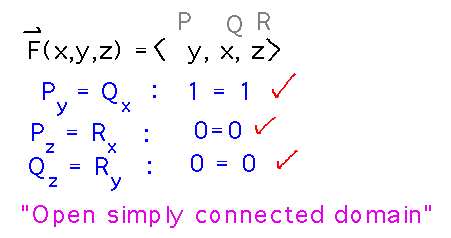
Show that F(x,y,z) = 〈 y, x, z 〉is conservative.
We can use the cross partial test again, with an important caveat: in order for the test to show that a field is conservative, the domain of the field has to be open and simply connected, i.e., have no hard boundary and have no “holes” where the field becomes undefined inside that boundary. This is the case for this F, so the test shows that it is conservative.
Next
Green’s theorem.
Read section 6.4