Misc
GROW STEM Talk
“Status of Women and Under-Represented Groups in various fields of STEM”
Led by Provost Stacey Robertson.
Thursday, April 19, 5:00 pm.
Newton 204.
Questions?
Line Integrals in Vector Fields
Theorem 6.5.
There’s another typo (in the PDF version, it’s fixed online) — try to find it and suggest a correction.
The third equation
![]()
should be
![]()
This result makes intuitive sense based on the idea that a line integral of a vector field is the integral of the components of the vectors in the direction of motion along the path. If you reverse that direction, the vector components negate.
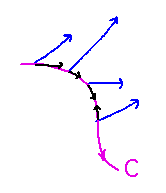
Examples
Space Rock, Continued
Recall the space rock and star from Friday. Consider another rock that is in orbit instead of falling towards the star. This rock moves from (2,0,0) to (0,2,0) along a quarter circle of radius 2, under gravitational field
![]()
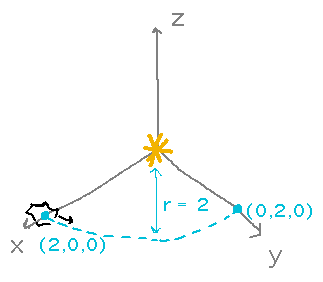
Calculate the work done on the rock by the star’s gravity.
We first need to come up with a parametric description of the path the rock follows. One is based on the standard parametric form for a circle, namely
![]()
Another possibility is to describe the quarter circle by the equation y = √(4-x2) and parameterize accordingly, with x ranging from 2 down to 0:
![]()
This works better in subsequent integrations than it might seem (try it), but I’ll finish this example using the first parameterization.
To start, find the derivative of r(t)
![]()
and then calculate the denominators from the gravitational field so it can be plugged into later expressions.
![]()
Now we can put these pieces together in an integral for work:
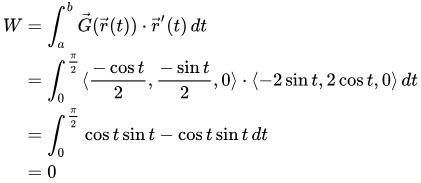
This result makes physical sense, because gravity hasn’t moved the rock closer to or farther from the star, so no work has been done.
A Line Integral with No Physical Significance
Let f(x,y) = 〈 x2, y2 〉 and r(t) = 〈 cos t, sin t 〉, 0 ≤ t ≤ π . Find the integral of F along r.
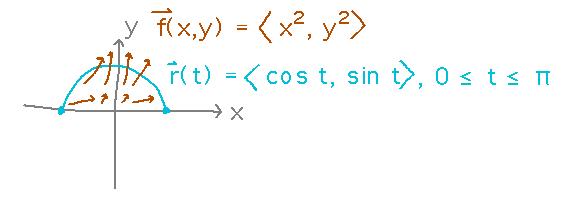
Start by finding the derivative of r(t)
![]()
and f(r(t))
![]()
Now we can integrate:
![]()
Integrate each part of the sum separately, using two different substitutions: u = cos t, du = -sin t dt and v = sin t, dv = cos t dt. Doing this turns the integral into
![]()
Next
Flux and circulation.
Read the “Flux and Circulation” subsection of section 6.2.