Misc
Calculus Bee
PRISM-sponsored calculus contest (probably single-variable).
Thursday April 19, 4:00 PM, place TBA.
Questions?
Scalar Line Integrals
Part of section 6.2.
Theorem 6.4
Gives formulas for calculating line integrals of 2- and 3-variable functions.
Unfortunately, it has typos.
Find and fix them. (Hint: the theorem follows directly from Theorem 6.3, which is written correctly.)
Correction: the second “=” in each of the main equations should actually be multiplication.
Example
Integrate z = 8 - x2 - y2 along...
- Path x = y from (0,0) to (2,2)
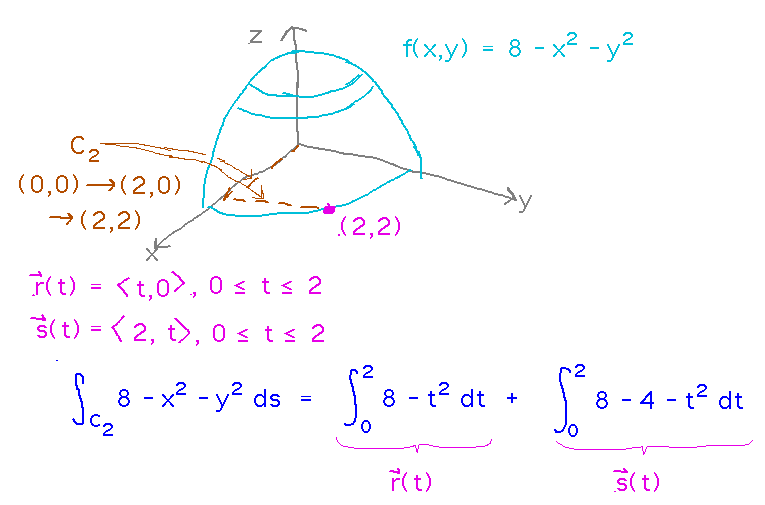
- Path y = 0 from (0,0) to (2,0) followed by x = 2 from (2,0) to (2,2)

For the x = y path, the first thing to do is figure out r(t), a parametric equation for the path. Any parameterization will do, the simplest is probably r(t) = 〈 t, t 〉.
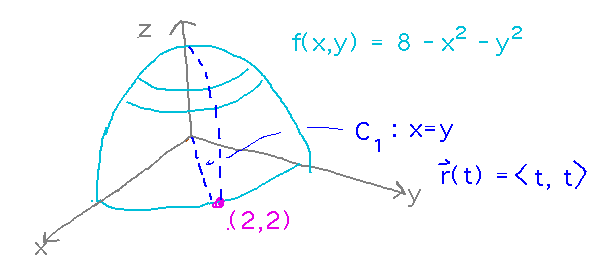
We also need to figure out what value t ranges over. We need to go from (0,0) to (2,2), which for the parameterization chosen would be t = 0 to t = 2. We can also express f in terms of r(t), and find the magnitude of r’(t), aka the square root of sums of squares of derivatives of component functions called for in Theorem 6.4:
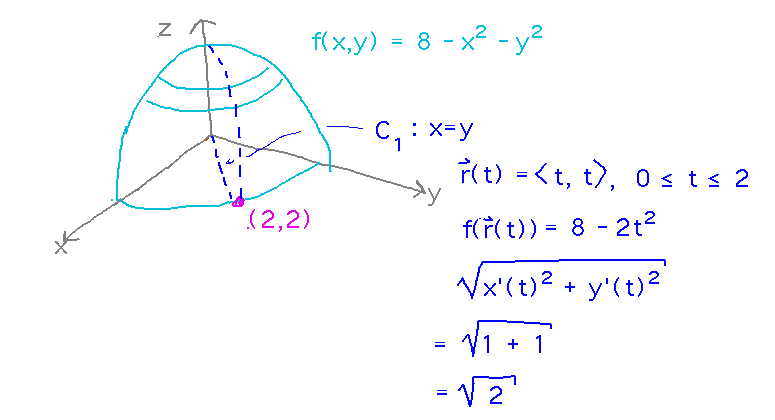
Finally, put these pieces together to evaluate the line integral:

For the second path, the key thing is that paths can be broken up into non-overlapping segments, and the integral over the whole path is the sum of the integrals over the segments (this follows from the fact that line integrals are Riemann sums, like all other integrals, and the sum along a path can be regrouped into the sum of sums along the segments).
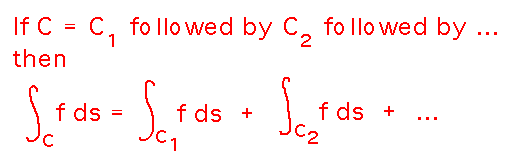
Now parameterize each segment of path 2 separately, integrate separately, and add the results. This is particularly easy to do because the magnitudes of the derivatives of both parametric forms are just 1.
Key Points
The idea of a line integral, i.e., an integral along a particular path through a function’s inputs.
How to evaluate scalar line integrals.
Next
Line integrals of vector fields
Read “Vector Line Integrals” in section 6.2.