SUNY Geneseo Department of Mathematics

Finding Centers of Mass

Monday, April 9

Math 223 04
Spring 2018
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Questions?

Center of Mass Via Integration

Recall the Pyramid of Peril:

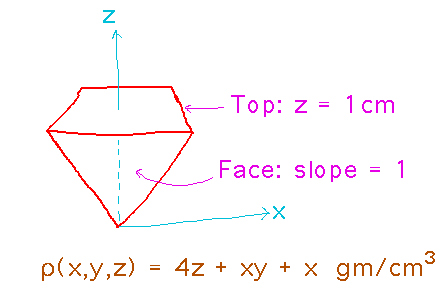
Inverted pyramid, 1 cm high, slope 1 sides, density at (x,y,z) = 4z + xy + x

Friday we figured out that the mass is 4 g. Now I want to figure out the center of mass, i.e., the point that has to be positioned directly above the tip to keep the Pyramid in balance.

Inverted pyramid with rho = 4z + xy + x, height 1 cm, sides have slope 1

The key equation is that for moment about a plane or axis, basically a sum of masses weighted by distance from the reference plane/axis (or a sum of distances weighted by the mass at that distance). From moments about the xy, xz, and yz planes you can find the z, y, and x coordinates of the center of mass by dividing by mass.

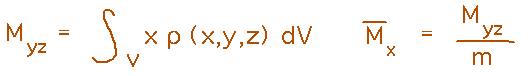
Moment about yz is integral over region of x times rho; x coordinate of center of mass is moment divided by mass

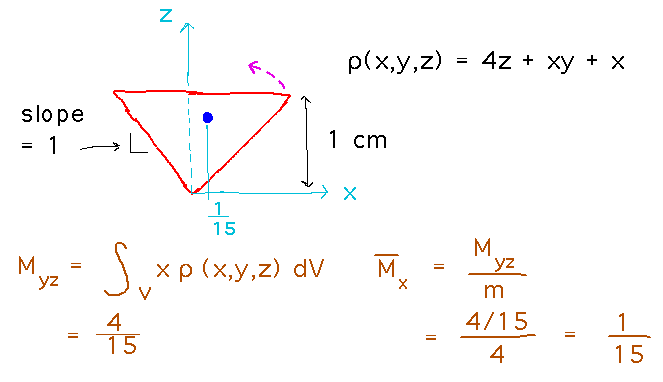
The first step is to figure out the bounds of integration needed to integrate over the Pyramid’s volume. Find a variable in terms of which it’s easy to calculate bounds on the other variables for tracing out points in the volume. In this case, it’s easy to see that z ranges from 0 to 1, and that at each z value the slopes of the sides of the Pyramid mean that x and y will range between -z and +z.

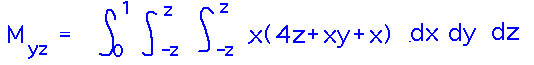
Integrate x times rho over z = 0 to 1, x = -z to z, y = -z to z

With the bounds in place, we can evaluate the integrals:

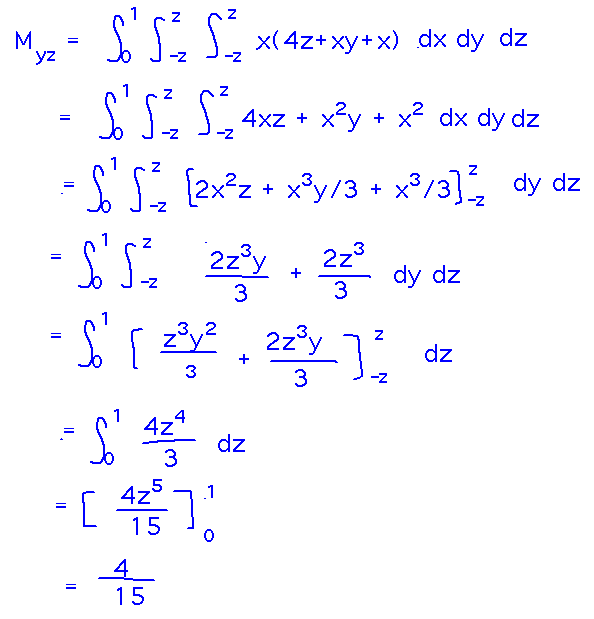
Integrating x times rho in three stages

With this moment we can find the x coordinate for the center of mass.

Inverted pyramid with x center of mass at 1/15

And we can similarly work out the y and z coordinates for center of mass. But having done one of these integrals by hand, take the more realistic route of evaluating the others with muPad or a similar tool. For example, here’s how we could have done the x coordinate with muPad:

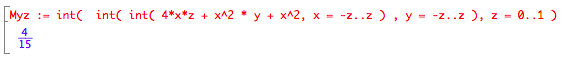
The int commands nested inside each other

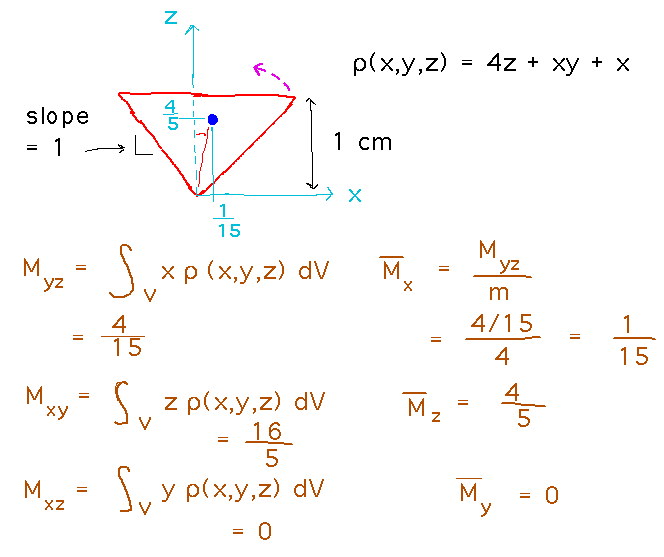
The final result is that the center of mass is at ( 1/15, 0, 4/5 ). So that’s the point that has to be directly above the Pyramid’s tip in order for the whole thing to balance. And we can even figure out what angle to rotate the Pyramid through to get there, namely tan-1( x / z ) = tan-1( 1/15 / 4/5 ).

Inverted pyramid with x, y, and z coordinates for center of mass

Key Points

An example of multiple integration and a corresponding physical quantity.

Using muPad (or other technology) to solve such problems.

Next

Multivariable vector valued functions — vector fields.

Read section 6.1 through “Drawing a Vector Field” (top of page 640 through bottom of page 651).

Bring muPad.

Next Lecture