Classifying Extreme Points

Return to Course Outline

Previous Lecture

Misc

Exam 2

Hour exam 2 is next Thursday, March 29.

It will cover material not covered on the first exam, through partial derivatives (e.g., curvature, arc length, multivariable limits, partial derivatives, tangents, etc).

The rules and format will otherwise be similar to the first exam, particularly the open-book, open-computer rule.

Questions?

Classifying Extreme Points

Find and classify the critical points of z = x³/3 - x - y².

Start by finding the derivatives of z, and looking for places they are 0 (or undefined):

which is 0 if x = ±1. Also,

which is 0 if y = 0. So the critical points have x = ±1 and y = 0, i.e., they are (1,0) and (-1,0).

Given the critical points, the discriminant / second derivative test can (sometimes) tell whether they are minima, maxima, or saddle points:

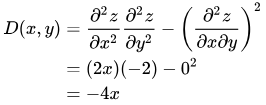
Using this equation, D(1,0) = -4, and D(-1,0) = 4. A negative discriminant indicates a saddle point, so point (1,0,-2/3) is a saddle point. A positive discriminant indicates either a maximum or minimum, depending on the sign of the second derivative with respect to x. In this case

which equals -2 when x = -1. The negative value indicates that this critical point corresponds to a maximum of the function. A plot of the function visually shows what these points look like:

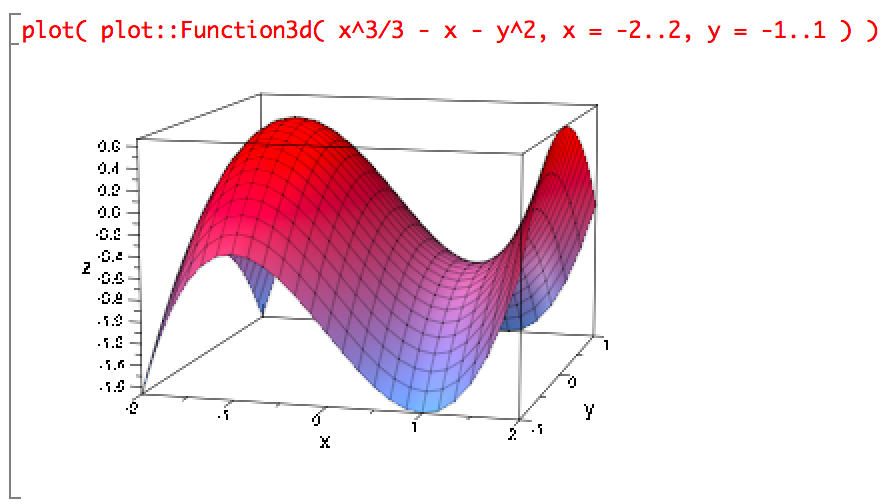
Does the second derivative used to test for a maximum or minimum when the discriminant is positive have to be the second derivative with respect to x? No, the logic behind it is exactly the same as the logic for the second derivative test for single-variable functions, namely that a negative second derivative indicates that the first derivative is decreasing, i.e., going from a positive value through 0 to a negative one, and thus signalling a local maximum in the function, while a positive second derivative indicates that the first derivative is increasing, thus indicating a a minimum. In a multivariable function, maxima and minima are high or low points no matter what direction you approach from, so the first and second derivatives with respect to y behave the same way around maxima and minima as the derivatives with respect to x do. The choice of second derivative with respect to x is therefore arbitrary, you could just as well use the second derivative with respect to y.

Absolute Extremes

Find the absolute maximum and minimum of z = x³/3 - x² + y² + 2y on the region -3 ≤ x ≤ 3, -2 ≤ y ≤ 2

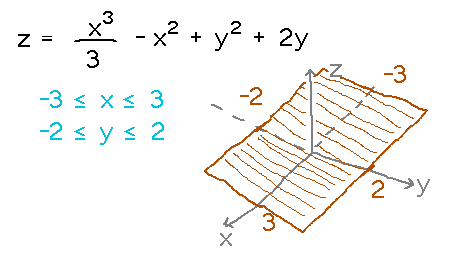
The basic strategy for finding absolute extremes is a generalization of that for single variable functions:

1. Find critical points in the region
2. Find maxima and minima around the boundary of the region (like checking the endpoints of an interval in the single-variable case)
3. Manually find the maximum and minimum function values for the points found in steps 1 and 2.

Next

Finish talking about absolute extremes.

Start talking about optimization and Lagrange multipliers, section 4.8.

Next Lecture