SUNY Geneseo Department of Mathematics
Wednesday, March 21
Math 223 04
Spring 2018
Prof. Doug Baldwin
Hour exam 2 is next Thursday, March 29.
It will cover material not covered on the first exam, through partial derivatives (e.g., curvature, arc length, multivariable limits, partial derivatives, tangents, etc).
The rules and format will otherwise be similar to the first exam, particularly the open-book, open-computer rule.
“Oh, the Places You Will Go”
(Identifying and mapping career trajectories and facilitators)
Dr. Amanda C. Bryant-Friedrich
Monday, March 26, 5:30 - 6:30 PM, Newton 204.
First subsections of section 4.7.
Characterize the points at which
is maximum or minimum. (Plotting this function produces a water-drop-like rippling wave, as below, and I use it in plotting exercises/examples in Math 230; the maxima and minima are the peaks and troughs of that wave.)
Intuitive analysis of the function suggests that the cosine term is the main thing that produces the wave, with the exponential term scaling it down as it gets further from the origin. So you’d expect the peaks to be where cosine is largest (i.e., x2+y2 = 0 or another even multiple of π), and the troughs to be where cosine is smallest (odd multiples of π). But this isn’t quite right because the exponential term is slightly larger just before these multiples of π and slightly smaller just after, which seems like it should shift the peaks/troughs slightly.
For a more precise and formal analysis, find critical points in the function, as they should correspond to the minima and maxima. Critical points occur where both first derivatives are 0, or at least one is undefined. So find the derivatives and solve for values of x and y that make them 0. Here’s the derivative with respect to x, the derivative with respect to y is very similar:
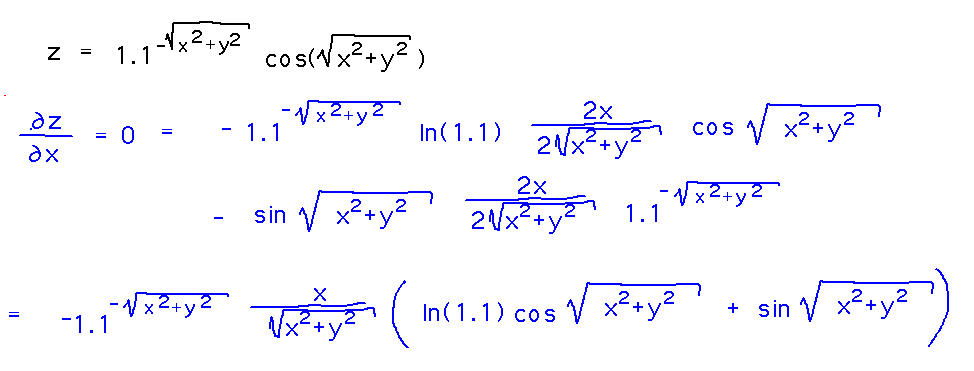
To figure out where this is 0, just find values of x that make each term in the product 0. The leading exponential term is never 0, the x/√(x2+y2) term is 0 when x is 0, and solving for values that make the last term 0 isn’t that hard:
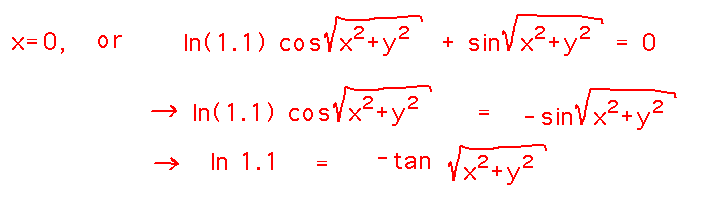
The ln 1.1 part of the solution reflects the shift in peaks and troughs I mentioned earlier: if that term were 0, peaks and troughs would occur where the tangent is 0, i.e. at any point whose distance from the origin is an integer multiple of π, as suspected intuitively. But since ln 1.1 isn’t quite 0, and because the tangent is negated, peaks and troughs actually occur where the tangent is slightly negative, i.e., just before multiples of π.
There are such things as critical points for multivariable functions, indicating possible extreme values much as they do for single-variable functions.
A second derivative test to tell what sort of extreme happens at a critical point.
Absolute extremes.
Start reading “Absolute Maxima and Minima” in section 4.7