Geneseo Math 223 04 Gradients

Misc

Colloquium on inverse problems rescheduled for this Thursday:

Sedar Ngoma, “An Overview of Inverse Problems.”

Thursday, March 22, 2:30 PM, Newton 203.

Extra credit as usual for 1-paragraph connections or other reactions.

Mid-Semester Course Evaluation

An informal, anonymous, survey to see how this course is working for you. Fill out or not as much or as little as you wish. But try to return them by Wednesday if you fill anything out.

Questions?

The Gradient

The latter parts of section 4.6.

The Basic Idea

Find the gradient of f(w,x,y,z) = wx² + 2xy + y/z + z²w³.

The gradient is just a vector of the partial derivatives of f, so start by finding those derivatives:

4-dimensional function and its 4 partial derivatives

Then put them into a vector (for 4-dimensional vectors I’ll put the components in the order w, x, y, z, since there’s no particular standard that says how to order them):

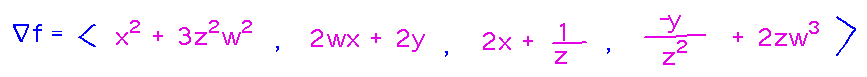
Vector containing 4 partial derivatives

Gradients and Directional Derivatives

In what direction should you move from (x,y) = (1,-1) in order to see z = 2x² - y² increase the fastest?

Point (1,-1) in the xy plane

The key insights are that the rate at which a function increases is its directional derivative, so this is basically asking to find the direction vector u that will make the directional derivative at (1,-1) largest. Furthermore, directional derivatives can be written as the dot product of the gradient and the direction vector, and that product will be largest when the angle between the vectors has a cosine of 1, i.e., the angle is 0. In other words, the gradient points in the direction of greatest increase!

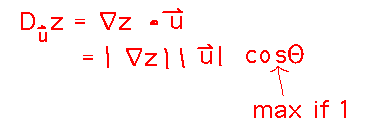
Direction derivative = gradient dot direction

So we can solve the problem by finding the gradient of z at (1,-1), and then normalizing it to a unit vector:

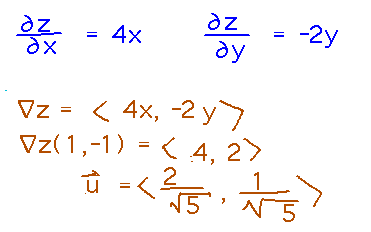
Partial derivatives make gradient, evaluate it at a point and find unit vector

Gradients and Normals

Find an equation for the tangent plane to x² + y² + z² = 1 at (1/2, -1/2, √2/2).

Sphere and its equation

The key idea here is to think of the surface as a level “curve” (level surface more accurately) of a function that needs 4 dimensions to graph completely.

Now remember that another property of gradients is that they are normal to level surfaces. So find the gradient of this function at the point in question, and use it as the normal in a plane equation:

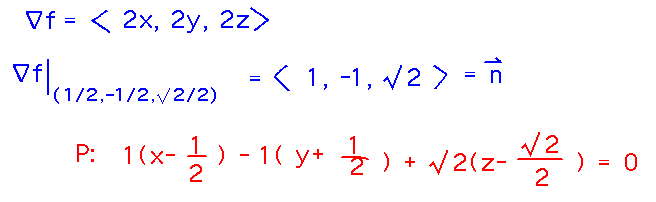
Components of gradient become coefficients of plane equation

Key Ideas

The gradient as a vector of partial derivatives.

A key property: the gradient points in the direction of greatest increase in the function.

A related key property: gradients are normal to level curves/surfaces.

Extreme values of multivariable functions.

Read the “Critical Points” and “Second Derivative Test” subsections of section 4.7.