Partial Derivatives

Return to Course Outline

Previous Lecture

Misc

Exam 1

Think of grades in the 40s as As, 30s as Bs, 20s as Cs, teens as Ds.

Median grade was 36.

Graded papers generally have explanations of mistakes, or complete solutions, as appropriate.

Question 3 (cylinder defined by lines parallel to <2,1,0> through z = y²) needs explanation: Since a cylinder is defined by parallel lines passing through a 2D curve, the phrase “curve z = y²” would ideally be interpreted as describing a 2D curve at some constant x value, e.g., 0, with lines parallel to <2,1,0> passing through it.

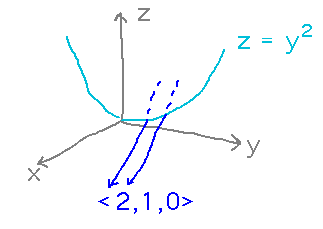
Then points on the cylinder are of the form (x,y,y²) + k<2,1,0> where x is your chosen x coordinate, y is a chosen y coordinate, and k is any constant you like. But there turned out to be lots of other reasonable ways to interpret “curve z = y²” and so I considered solutions that used arbitrary x coordinates to be OK (but not perfect), as long as they didn’t describe some unjustifiable way of computing x.

Questions?

Partial Derivatives

Section 4.3.

Examples

Find ∂z/∂x and ∂z/∂y for z = x² + 2xy - y².

The main thing to remember here is to treat variables other than the one you’re differentiating with respect to as if they are constants.

Find ∂f/∂x and ∂f/∂y for f(x,y) = e^xy + y sin(x²).

Here you need to use the chain rule for single-variable derivatives, which is fine when finding partial derivatives.

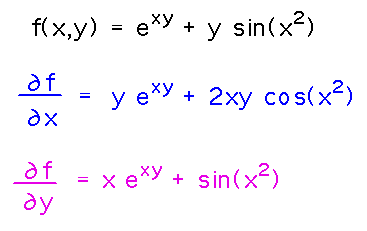
Find ∂f/∂x, ∂f/∂y, and ∂f/∂z for f(x,y,z) = xy + 2yz + 3xz.

There are more variables, but you can still find the partial derivatives by treating all variables except the one being differentiated with respect to as constants.

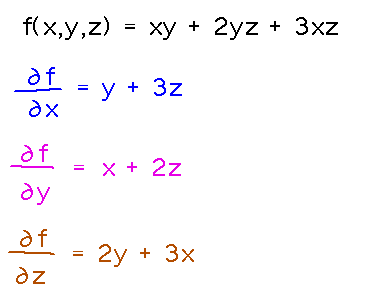
Higher-Order Partial Derivatives

Find all the second derivatives of f(x,y) = x²y - 3xy + xy².

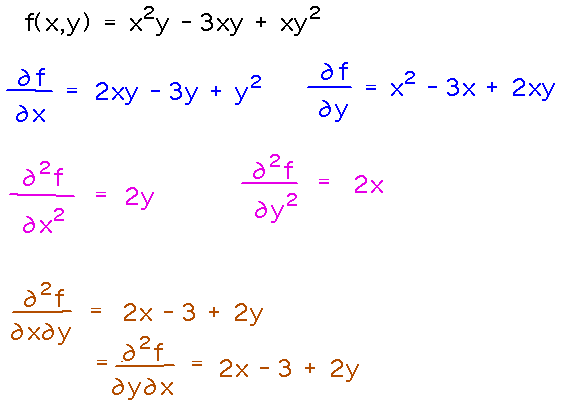
Notice the “mixed second derivatives,” found by differentiating first with respect to x and then with respect to y, or vice versa.

That these are identical is an example of “Clairaut’s Theorem,” also known as the “mixed derivative theorem,” which says mixed second order derivatives don’t depend on the order in which you evaluate them, as long as both are continuous near the point at which you evaluate them.

Key Points

Evaluate partial derivatives much as you would single-variable ones, just treating every variable except the one you’re differentiating with respect to as a constant.

Next

Tangent planes and linearization.

Read section 4.4.

Next Lecture