Limits of Multivariable Functions

Return to Course Outline

Previous Lecture

Questions?

Multivariable Functions

Auditorium “field trip.”

Think of the floor as the xy plane, and the curved ceiling as the surface of a multivariable function you can walk around under.

To walk along a level curve, walk in a straight line parallel to the long dimension of the ceiling: a level curve is a curve along which the function’s value doesn’t change, i.e., a path along which the height of the ceiling immediately above you neither increases not decreases.

Also notice that level curves are paths on the floor, i.e., the xy plane, not the surface -- you don’t have to climb to the ceiling in order to walk along a level curve.

Limits of Multivariable Functions

Section 4.2

Limits

Find lim_{(x,y)→(1,0)} xy / (x² - y²).

One way to think about this is to set x = 1 and then take the limit just as y approaches 0 (or, in more detail, take the limit as x approaches 1 first, and then take the limit of the result as y approaches 0). This follows from the various limit laws for multivariable functions, which are just generalizations of the 1-variable limit laws.

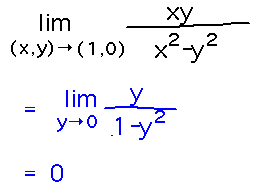
Find lim_{(x,y)→(0,0)} (x² - y²) / (x+y).

One idea is to consider x and y approaching (0,0) along several paths, and see what limit(s) you reach.

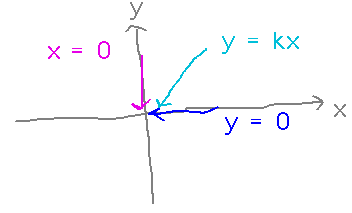
This is a powerful idea for recognizing when a limit doesn’t exist, by looking to see if the limits along different paths differ. But unlike the 1-variable case where you can sometimes find a limit by finding right and left limits and seeing if they agree, there are an infinite number of paths along with you can approach a point, and you can’t check them all.

But you can use algebra to rewrite the function into a form to which you can apply limit laws:

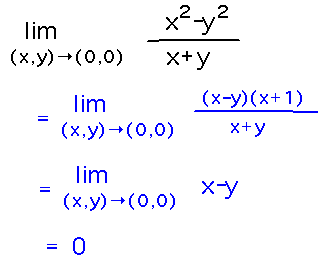
Find lim_{(x,y)→(0,0)} (x + xy - y) / (x + 2y), or show that it doesn’t exist.

In this case the limit doesn’t exist, as can be seen by considering two paths:

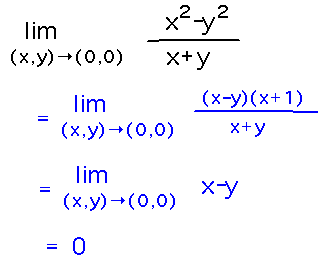
Continuity

Find an example of a point at which (x + xy - y) / (x + 2y) is continuous.

Continuity at a point requires the same 3 things it does for other kinds of functions:

1. The function is defined at the point
2. The limit is defined at the point
3. The function and the limit are equal.

Thus, for example, the function is continuous at (1,1), because both it and its limit are 1/3 there.

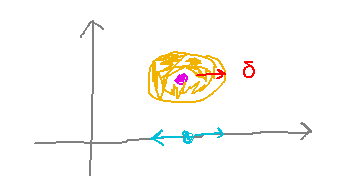
You can also think of continuity, and more significantly limits, in terms of how the function behaves over a small circle around the point. This is analogous to 1-variable limit definitions that talk about a small interval extending δ units to either side of an x value, except in 2 dimensions what it means to be within δ units of a point is to be within a circle of radius δ around the point.

Key Points

Limit laws exist for multivariable functions, and are very much like limit laws for 1-variable functions.

Other familiar laws often, but not always, work.

The two-path test for non-existence of a limit.

Essentially the same definition of continuity applies to multivariable functions as applied to other functions you’ve seen.

Next

Partial derivatives

Section 4.3

Next Lecture