Motion in Three Dimensions

Return to Course Outline

Previous Lecture

Misc

The first hour exam is Monday, Feb. 26.

I’ve put a sample exam from last time I taught this course in Canvas. But note that it was designed for a longer class time than we have, so yours will have fewer questions than the sample. But your questions should be of similar style and difficulty to the sample.

It will cover material from the beginning of the semester through calculus of vector valued functions (but not arc length or curvature), i.e., problem sets 1 through 4, i.e., textbook chapter 2 plus sections 3.1 and 3.2.

4 to 6 short-answer questions, roughly comparable in style and difficulty to medium-difficulty problem set questions.

You’ll have the whole class period to do the test.

Open book, open notes, open computer for reference, but closed person. Open calculator too.

Questions?

Motion and Vector Valued Functions

Section 3.4.

Puzzle

Find an example of 3D motion in which the speed is constant but the velocity isn’t. What are the corresponding position and acceleration functions?

A conceptual example could be a car climbing a hill: as the hill gets steeper the direction of the velocity vector becomes more upward, but the car’s speed (i.e., the magnitude of the velocity vector) could stay constant.

An example we can more directly work with might be v(t) = 〈 sin t, cos t, 1 〉. To tell if the speed is constant, calculate the magnitude of this function and see if it’s a constant:

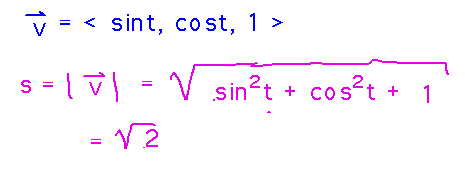
And it is.

Finish with this example by finding the position function (indefinite integral of velocity) and acceleration (derivative of velocity):

Theory

Derive the equations for tangential and normal components of acceleration, i.e.,

• a_T = (v•a)/|v| = a • T
• a_N = √(|a|²-a_T²) = | v × a | / |v|

The first comes from the idea that a_T is the component of a in the direction of T, something you can compute with a dot product and the equation a•b = |a| |b| cos Θ. In this case, note that v is parallel to T, so (v•a)/|v| is |v| |a| cos Θ / |v| =|a| cos Θ, or note that v/|v| = T which is of unit length so its length doesn’t need to be divided out after computing a•T.

The first formula for a_N comes from the Pythagoren Theorem and the observation that a_N is the length of one leg of a right triangle whose other leg is a_T and whose hypotenuse is |a|.

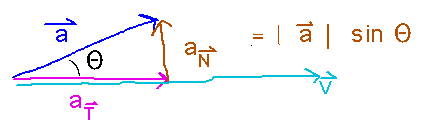
The second formula for a_N comes from realizing that the a_N side of that same right triangle has length |a| sin Θ, which can be calculated using the rule that | a × b | = |a| |b| sin Θ.

Key Points

Vector valued functions can be used to describe motion.

The derivative/antiderivative relationship between acceleration, velocity, and position underlies all such modeling of motion.

Next

Preparing for the Test

Canvas discussions based on problem-solving scenarios, particularly differentiation and integration of vector valued functions, instead of in-person classes this Wednesday, Thursday, or Friday.

See the discussions in Canvas at “Calculus of Vector Valued Functions 1” and “Calculus of Vector Valued Functions 2.”

After the Test

For Wednesday, February 28.

Introduction to multivariable functions.

Read section 4.1.

Next Lecture