Misc
The first hour exam is Monday, Feb. 26.
It will cover material from the beginning of the semester through calculus of vector valued functions (but not arc length or curvature), i.e., problem sets 1 through 4, i.e., textbook chapter 2 plus sections 3.1 and 3.2.
4 to 6 short-answer questions, roughly comparable in style and difficulty to medium-difficulty problem set questions.
You’ll have the whole class period to do the test.
Open book, open notes, open computer for reference, but closed person. Open calculator too.
Questions?
Curvature
Second half of section 3.3.
Curvature is basically a (magnitude of a) derivative of the curve’s unit tangent vector with respect to distance along the curve, reflecting the fact that the more sharply a curve turns, the greater the change there has to be in its tangent over a shorter distance:
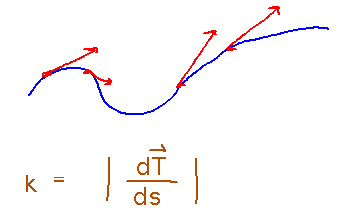
But this isn’t a computationally useful definition, so use any of several equivalent equations to actually compute curvature.
The Main Idea
Find the curvature function for r(t) = 〈 t, t2, t 〉.
The first step is to decide what curvature calculation to use. The two most plausible for this 3D vector valued function are one based on the derivative of the unit tangent vector, and one based on the cross product of derivatives of r. The second of these is much easier to work with in this problem.
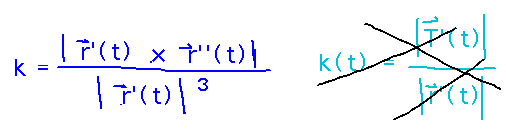
To use this formula, we need the first and second derivatives of r, their cross product, and some magnitudes:
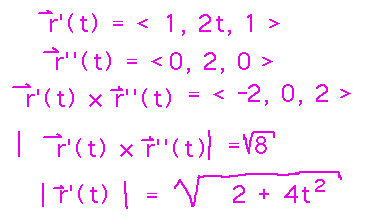
Plugging those quantities into the curvature formula gives curvature as a function of t:
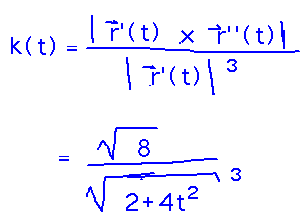
What is the curvature when t = 0? What does it mean?
Plug t = 0 into the curvature function to get a number, but what does that number mean? Formally it’s the rate of change in the unit tangent vector per unit distance along the curve. Informally it measures how sharply the curve is turning. As something of a balance between those, it’s also related to (specifically, it’s the reciprocal of) the radius of the circle the curve is “instantaneously” turning around, i.e., the radius of a circle tangent to the curve and just “fitting” into it (the so-called “osculating circle”):
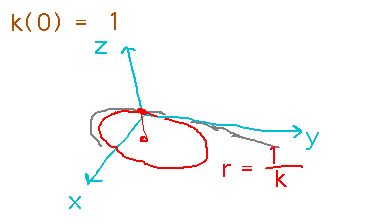
The Principal Unit Normal
What is its geometric significance? It’s a unit vector that points from a curve towards the center of the osculating circle, i.e., points in the direction the curve is turning at a particular point. It’s also thus the direction of the centripetal force a physical object would feel making that turn.
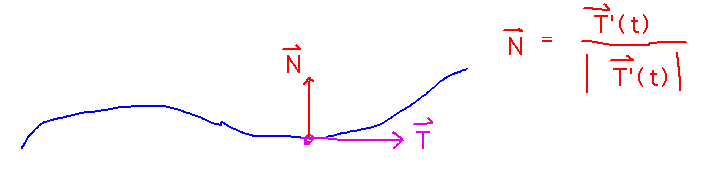
Key Points
Curvature and the standard unit normal provide information about the geometry and intensity of curves in a vector valued function.
There are equations for finding them, although they are often computationally ugly.
Next
Applications of vector valued functions and their calculus to motion.
Read section 3.4.