SUNY Geneseo Department of Mathematics

Arc Length

Wednesday, February 14

Math 223 04
Spring 2018
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Misc

Colloquium

Friday, February 16, 2:30. Newton 203.

“From Differential Equations to Difference Equations and Everything Else in Between.”

Differential equations define a continuous function in terms of its derivative(s); difference equations define a discrete function in terms of its difference(s).

Derivatives lead to a continuous function; differences to a discrete one

Billy Jackson, SUNY Geneseo.

Extra credit for going and writing a short reaction.

Questions?

Integration with muPad

Vector valued functions that you integrate with muPad need to be defined as matrices of functions, nominally n-row-by-1-column.

Define matrices with the function matrix( rows, columns, [ components ] ) where rows is the number of rows, columns is the number of columns, and components is a comma-separated list of components.

Then the int function computes integrals, either definite or indefinite depending on whether you attach a range of values to the integration variable.

int and matrix functions evaluate an indefinite integral

int and matrix functions evaluate a definite integral

muPad will actually integrate any matrix of functions.

int integrates matrices of functions of various shapes

Arc Length of Space Curves

Theory

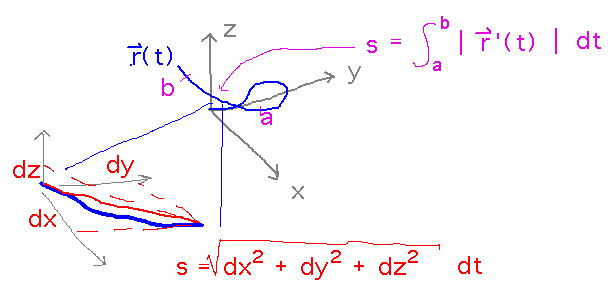
What’s the justification for the arc length formula?

It comes from approximating very short segments of the curve as straight lines and applying the distance formula, in a Riemann sum.

Short segment of curve has x, y, z lengths dx, dy, dz.

Example

Find the arc length of r(t) = 〈 sin 3t, cos 3t, 1 〉 from t = 0 to 2.

Start by finding the derivative of r:

derivative of < sin(3t), cos(3t), 1 > = < 3cos(3t), -3sin(3t), 0 >

Then evaluate the arc length integral, taking advantage of a trigonometric identity to simplify it:

Integral from 0 to 2 of sqrt( 9cos^2(3t)+9sin^2(3t) ) equals integral from 0 to 2 of 3

And finally evaluate the integral:

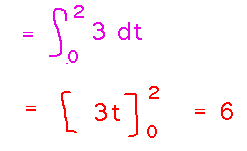
Integral from 0 to 2 of 3 is 6

Arc Length Parameterization

Consider r(t) = 〈 t2, t2, t2 〉.

This function defines a straight line, i.e., the quadratic terms don’t affect the shape of the curve.

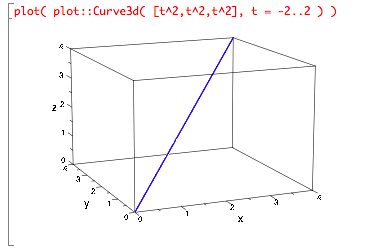
Plotting <t^2,t^2,t^2> yields a straight line

What they do affect is how “fast” you move along the curve at different t values. The value of t isn’t a guide to how far along the curve you have moved.

Some times you want to parameterize a curve in such a way that the parameter value tells you how far you’ve moved, e.g., “if t is now twice what it was before, I must be twice as far along the curve as before.” The arc length parameterization does this.

The strategy for finding a parameter that corresponds to distance:

  1. Find a function s(t) that gives you distance along curve in terms of t.
  2. If s(t) can be inverted, you can get an expression, t(s), for t in terms of distance.
  3. Plug that expression into r( t(s) ) to get position in terms of distance.

Here’s how that works for the function above. We’ll use the basic arc length definite integral, but with the upper bound on the integration being t and the lower bound being an arbitrary starting t value -- let’s use 0, though it could be anything. Then rename the variable inside the integrand to avoid confusion with t as the upper bound. The overall result is a function of t that integrates arc length from 0 to t, i.e., finds the length of r from parameter value 0 to parameter value t, which is exactly what we wanted.

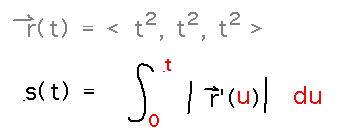
r(t) = <t^2,t^2,t^2>, s(t) = integral from 0 to t of magnitude of r'(u)

To use this on r(t) = 〈 t2, t2, t2 〉we need r’(t) =〈 2t, 2t, 2t 〉, or〈 2u, 2u, 2u 〉after renaming the parameter. Now plug that into the arc length integral and integrate:

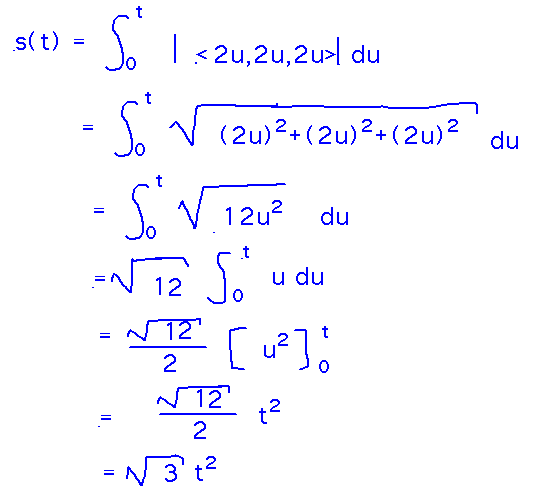
Integrating magnitude of r(u) from 0 to t yields sqrt(3) t^2

Now we have distance (s) as a function of t. To invert this and get t as a function of distance, rewrite to “solve” for t:

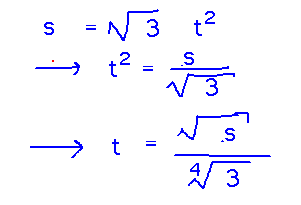
If s = sqrt(3) t^2 then t = sqrt(3) over the 4th root of s

Finally, replace t in the original definition of r with the expression for t in terms of s to get the arc length parameterization of the curve:

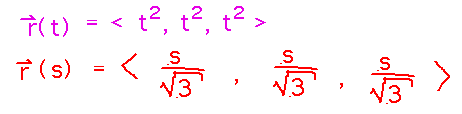
r(s) = < s/sqrt(3), s/sqrt(3), s/sqrt(3) >

Key Points

The arc length formula comes from the distance formula.

Using the formula to find arc length.

The arc length parameterization lets you express positions on a curve in terms of distance along that curve from some starting point.

Next

Curvature.

Read “Curvature” and “The Normal and Binormal Vectors” in section 3.3.

Next Lecture