Lines

Questions?

Lines

Parts of section 2.5

Basic Equations

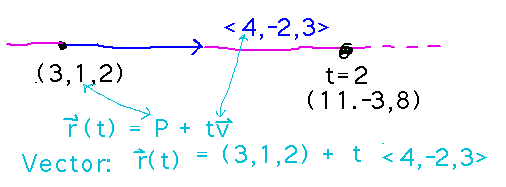
Give a vector equation for the line in direction 〈 4, -2, 3 〉 through point (3,1,2). How about parametric and symmetric equations?

The general vector equation for a line through point P in direction v is r(t) = P + tv. Here P = (3,1,2) and v = 〈 4, -2, 3 〉. Note that t is a variable that in general needn’t be solved for, although by plugging values in for t you can find points on the line.

The parametric equations for the line are really just the vector equation explicitly broken into x, y, and z parts:

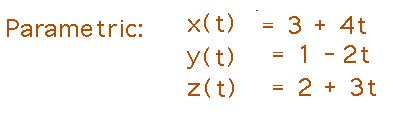
Finally, the symmetric equations rearrange the parametric ones to isolate t, and recognize that all those t’s have to be equal:

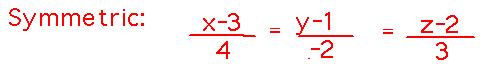
Using the Equations

Line/Plane Intersection

Where does the line r(t) = (3,-1,10) + t〈-2,4,2 〉 intersect the x = 0 plane?

Solve the parametric equation for x to find t when x = 0, then plug that t into the y and z equations to find the y and z coordinates of the intersection.

Line/Line Intersection

A more complicated intersection problem: Do the lines r₁(t) = (0,1,0) + t〈1,1,1 〉 and r₂(t) = (2,0,1) + t 〈0,3,1 〉intersect? If so, where?

Parameterize each line by its own variable, say t and s, then use the parametric equations as a system that can be solved for the t and s (if any) that make the two sets of coordinates equal. If you find such a t and s, plug one of them back into its parametric equations to find the intersection point.

Distance from a Line to a Point

Fearless space traveler Spacey is fleeing the evil alien starbase. Spacey is making for planet G’nseo, which lies at 〈8,2,-2〉 relative to the starbase. Unfortunately, Spacey is actually moving in direction 〈5,1,0〉. How close to G’nseo does Spacey get?

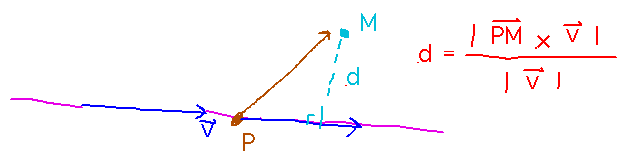
The key equation here is the one for the distance from a point to a line:

Key Points

The equations for describing lines in 3D space.

Use the parametric/vector equations to solve for t value(s) at which lines intersect other lines or surfaces.

The equation for the distance from a point to a line.

Next

Planes.

Read the rest of section 2.5 (subsections “Equations for a Plane” and “Parallel and Intersecting Planes”)