Misc
Colloquium
“Waring’s Problem over Finite Fields.”
Background: Every positive integer can be written as a sum of 4 perfect squares, e.g., 4=12+12+12+12, 8 = 22+22+02+02, etc. Waring generalizes this to any power, not just squares: for every n, there is g(n), such that every positive integer can be written as a sum of g(n) nth powers.
Yesim Demiroglu, University of Rochester.
Thursday, February 1, 2:30 PM, Newton 203.
Extra credit for going and writing a paragraph or so about connections you make to the talk.
Questions?
When using the right-hand rule to find the direction of the cross product u × v, turn your fingers through the smaller of the 2 angles between u and v.
The Cross Product
Section 2.4.
Basic Calculations
Find 〈1,3,2〉 × 〈3,-2,4〉
Use the definition of cross product, namely 〈v1,v2,v3〉 × 〈u1,u2,u3〉 =〈 v2u3-u2v3, -(v1u3-u1v3), v1u2-u1v2 〉to expand this into the appropriate differences of products:
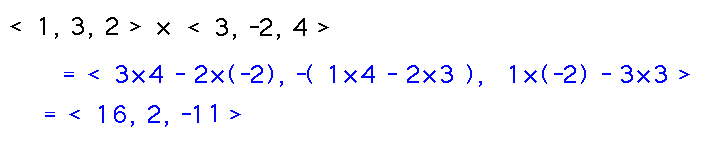
How do you remember the formula (assuming you don’t want to just look it up when you need it, and don’t have a calculator that will do it)? One of many mnemonics is writing the components of the vectors above each other, starting with the second component, and repeating it again at the end, and computing differences of products on the down-and-left diagonals minus products on the up-and-right diagonals. Another is the determinant mnemonic given in the text:
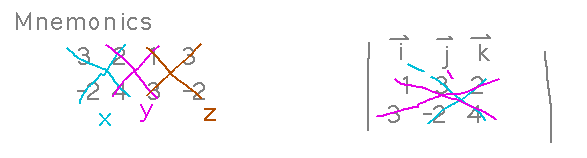
Applications
Perpendicular Vectors
The cross product of v and u is perpendicular to both v and u, so cross products have a lot of uses in situations where you need a vector perpendicular to 2 others.
For example, in electromagnetism where the force a magnetic field exerts on a moving charged particle is perpendicular to the field’s direction and the direction of motion.
Or video game designers with “gaze” and “up” vectors can make a complete coordinate system in which the player sees the game world if they can find a vector perpendicular to “gaze” and “up.”
Using our results from the dot product (to 2 decimal places), suppose a player is looking in direction〈0.67, -0.67, 0.33〉 and so has an “up” vector of〈-0.23, 0.23, 0.94〉. Find a vector in the direction the player perceives as “right.”
Use the formula above for cross product:
〈 0.67, -0.67, 0.33〉 ×〈 -0.23, 0.23, 0.94〉
=〈 -0.67 × 0.94 - 0.33 × 0.23, -(0.67 × 0.94 - 0.33 × -0.23), 0.67 × 0.23 - (-0.67) × (-0.23) 〉
=〈-0.706, -0.706, 0〉
Area
The magnitude of a cross product can be calculated from the magnitude of the vectors and the angle between them:
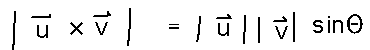
This turns out to be exactly what you need to find the area of a parallelogram with two sides defined by the vectors in question:
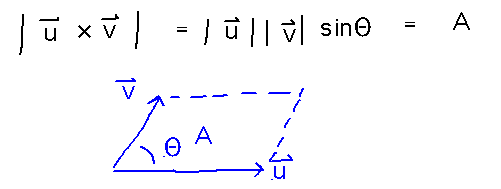
Torque
Torque is an analog of force for making something rotate. Informally it’s the product of the distance from the rotation axis at which a force is applied, and the component of that force perpendicular to the line from the center of rotation to that point. This again turns out to be the magnitude of the cross product of the distance vector and the force vector. This isn’t really surprising; the precise technical definition of torque is exactly that cross product.
So why do people only push or pull on wrenches perpendicular to the handle (contrary to the problems that textbook authors like to pose)?
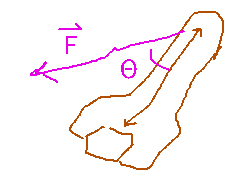
Because that angle maximizes the sinΘ term in the magnitude of the cross product, i.e., of the torque.
Key Points
Cross product formulas and their mnemonics.
Applications of cross products, notably for finding perpendiculars, areas, and torques.
Next
Defining and working with lines in 3 dimensions.
Read subsections “Equations for a Line in Space” through “Relationships between Lines” of section 2.5. (Pages 184 through most of 192 in the PDF book; 3 subsections total).