SUNY Geneseo Department of Mathematics
Friday, January 26 - Monday, January 29
Math 223 04
Spring 2018
Prof. Doug Baldwin
There’s a new extra credit opportunity for a “real-world math bounty”: find examples in daily life, etc., of ideas from this course. See the syllabus or Jan. 28 Canvas announcement for details.
You can get extra credit equivalent to up to 1/5 problem set for the math colloquium Jan. 26, 2:30, Newton 214. Write a paragraph about connections you make to the talk. “Due” by final exam.
There will be similar offers for other colloquia this semester.
The dot product seems to have two definitions: as the sum of the products of corresponding components, or as the product of two vectors’ magnitudes and the cosine of the angle between them. Which is it?
Different authors differ in which they give as “the” definition, but they always derive the other from whichever they start with.
Our text uses the sum of products as the definition and derives the product of magnitudes and cosine.
In practice you will probably use both in different problem-solving contexts.
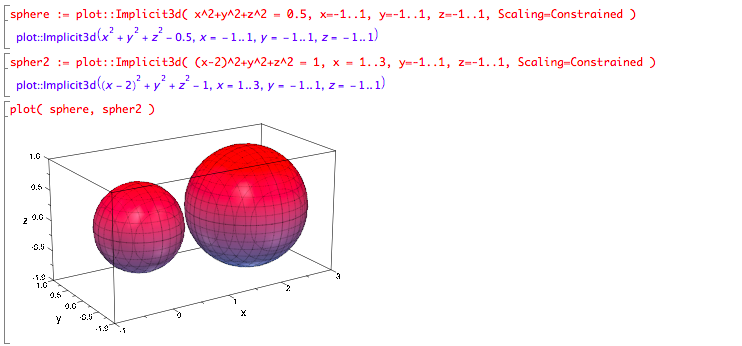
You can name the results of muPad commands in order to refer to them later, using syntax of the form
name := command
For example...
Section 2.3.
There’s a Google spreadsheet that we all share for doing the calculations for the following examples.
Find the dot product of u = ⟨3,-2,4⟩ and v = ⟨2,6,-3⟩
The key idea is that the dot product is the sum of the products of corresponding components of the vectors.
See the “Warm-Up” part of the spreadsheet to see the calculation carried out.
Fearless space traveler Spacey is fleeing the evil alien starbase. Spacey is making for planet G’nseo, which lies in direction ⟨4,1,-1⟩ from the starbase. Unfortunately, Spacey is actually moving in direction ⟨5,1,0⟩. What is the angle between Spacey’s actual and intended directions?
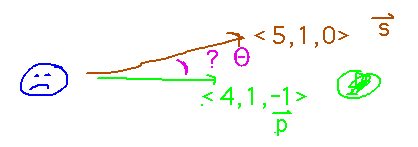
The key idea here is that dot product can also be expressed in terms of the angle between two vectors:
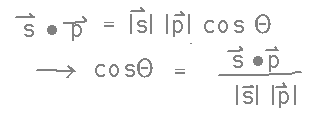
Carrying out the calculation (in the “Spacey” section of the spreadsheet) gives an angle of about 14 degrees.
What if it’s fearless space-time traveler Dr. Whowhatwhenwherewhyandhow, fleeing in direction ⟨5,1,0,-1⟩ when the correct direction is ⟨4,0,0,-2⟩?
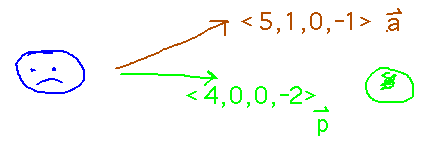
Dot products and their properties apply in any number of dimensions, so you can calculate this just as you did for the 3-dimensional space traveler, except for using 4 components in each vector. See the “Dr.” section of the spreadsheet for the calculation.
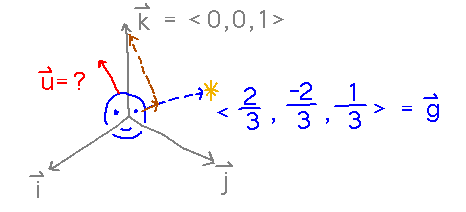
Thursday we saw how to find a vector for the direction a video game character is looking. Another vector that the video game programmers typically want is one pointing in the direction the character sees as “up.” One way to do this, based on the idea that video game characters usually have more or less horizontal gaze directions, is to take “up” to be a unit vector in the direction of the component of k that is perpendicular to the gaze vector.
If a character is looking in direction ⟨ 2/3, -2/3, 1/3 ⟩, what would the “up” vector be?
The basic scenario has a viewer looking slightly up from the horizontal in gaze direction ⟨ 2/3, -2/3, 1/3 ⟩. We want to find an “up” vector, i.e., a unit vector through the top of the viewer’s head. We can do this by splitting k into 2 components, one parallel to the gaze vector and one perpendicular to it. The “up” vector is then a unit vector parallel to the perpendicular component:
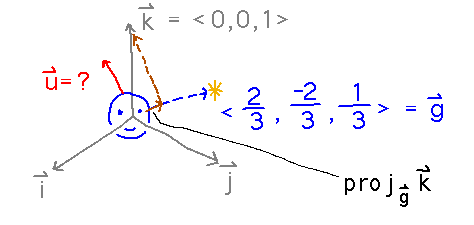
The key to doing this is to realize that the parallel component of k is the projection of k onto the gaze vector:
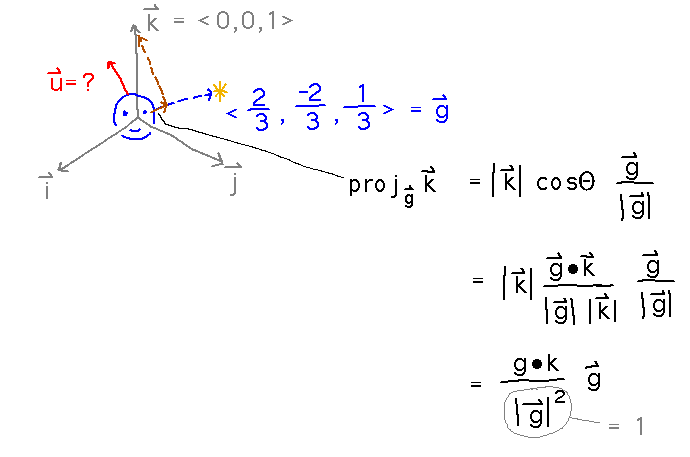
The textbook provides a formula for finding this projection, which we can simplify a bit because we know that both k and the gaze vector are unit vectors:
Now the perpendicular vector is k minus the projection:
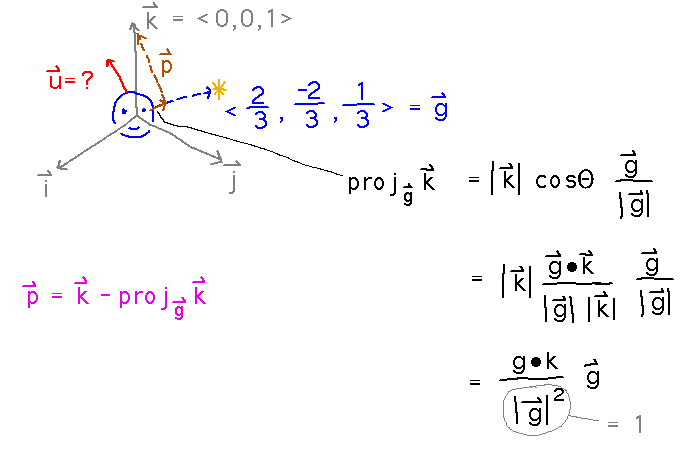
And finally the unit “up” vector is p scaled by its own magnitude:
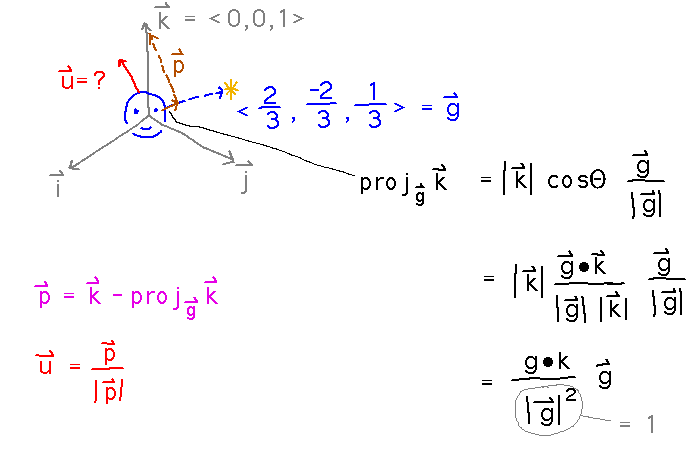
See the “Projection” section of the dot product spreadsheet for numerical calculations based on these ideas.
To verify that the vector you found is perpendicular to ⟨ 2/3, -2/3, 1/3 ⟩, see if its dot product with ⟨ 2/3, -2/3, 1/3 ⟩ is 0. It is (see the spreadsheet), so the vectors are orthogonal.
But beware that “orthogonal” means that the dot product is 0. This will happen either because the vectors are perpendicular, or because one or both is ⟨0,0,0⟩. Be sure when interpreting orthogonality as perpendicularity that you know both vectors are non-0 (as they are in this case).
The formula for dot product as a sum of products of components of two vectors.
The connection between dot products and the angle between two vectors.
The connection between dot products and projections of vectors onto each other (which follows from the connection between dot product and angle).
Another kind of vector product, the cross product.
For Wednesday, Jan. 31, read section 2.4.