Misc
Final
Sample questions are now on Canvas.
Friday, December 14, 8:00 AM.
Comprehensive, but with emphasis on material since last hour exam (e.g., multiple integrals, line integrals, vector fields, Green’s Theorem, etc.)
Designed for 2 hours, you’ll have 3 1/3.
Rules and format otherwise similar to hour exams, especially open-references and calculator/computer rules.
I’ll bring donuts and cider.
Review Session
11:30 - 12:30, Fraser 202A (our usual classroom), tomorrow.
SOFIs
7 responses. Thank you!
But there’s still time to submit more, and they’re helpful to me.
Review
More or less focused on material in the last problem set (e.g., line integrals in vector fields, Green’s theorem, etc.)
Question 1 Part 3
In particular, how to determine if the field in question is conservative, and if so, how to use that fact.
If the field is conservative, you might want a potential function to use with the fundamental theorem. So start by trying to find that function, i.e., asking whether the field is the gradient of some function, and if so what function.
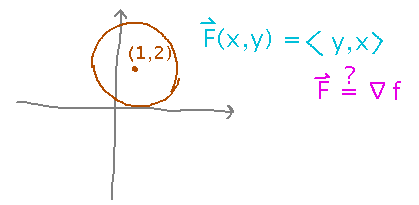
Use our usual process of alternating integrations and differentiations to find a supposed potential function whose partial derivatives form the components of the field:
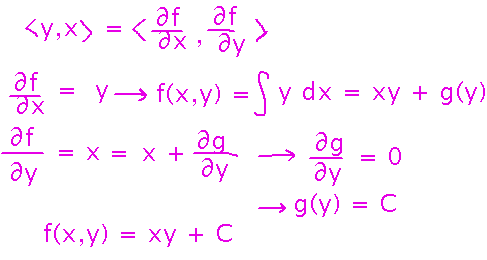
Having successfully found a potential function, you can conclude that the field is conservative. And further, realizing that the path around which you’re integrating is closed, you don’t even have to evaluate the potential function: circulation integrals of conservative fields around closed paths are always 0.
Potential Functions
Another example of finding a potential function, more challenging than just 2 dimensions.
Consider one of the book’s exercises: is F(x,y,z) = ⟨ yez, xez, xyez ⟩ conservative, and if so what is its potential function?
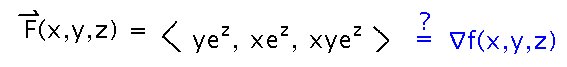
Start with the x component of the field. If there is a potential function, this component must be its derivative with respect to x, so integrate with respect to x to get a first version of the potential function:

This leaves us with a potential function with an unknown term g(y,z). To learn more about it, see how the derivative of the potential function with respect to z compares to the third component of the field (if there isn’t a potential function, this choice of looking at the z component next felt likely to reveal that fact sooner than looking at the y component would), and what g(y,z) would have to be to make them equal:
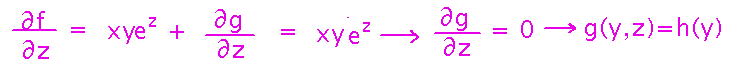
Now we have a better approximation to the potential function, but with an unknown term h(y). Find it by comparing the derivative of f with respect to y to the second component of the field.
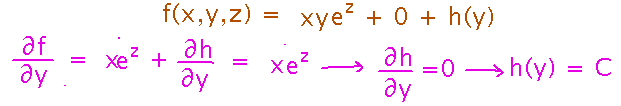
Finally, we have the complete potential function (or as complete as possible, there’s still a constant of integration):
![]()
Regular vs Line Integrals
What is the difference between a regular integral and a line integral?
A regular (single-variable) integral basically integrates a function as you move along an axis, whereas a line integral integrates a function as you move along an arbitrary path through its inputs.
Choosing a Method
A comparison to ways to evaluate vector line integrals:
| Standard Method | Fundamental Theorem | Green’s Theorem | |
|---|---|---|---|
| Always Usable | Yes | ||
| For Conservative Fields | Yes | Yes | Sometimes |
| For Closed Paths | Yes | Sometimes (Integral=0) | Yes |