General Review

Return to Course Outline

Previous Lecture

Extended Math Learning Center Hours

9:00 AM - 2:00 PM today

9:00 AM - 3:30 PM on final exam days through Monday (no hours Tuesday)

7:00 PM - 10:00 PM Sunday.

What Do You Want to Talk About?

Bounds for Multiple Integration

How to find bounds for the integral in problem set 10 problem 3, and convert to polar form.

The problem asks you to find the mass of a certain cylinder, given its dimensions and a density function:

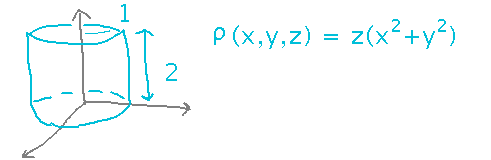
Start with the generic equation for mass from density, to give yourself a framework to work in:

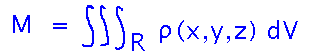
Now start fleshing out the general form by thinking about bounds for the integrals. The integral in the z dimension is easy, but when you get to x and y the fact that they define a circle starts to make things seem ugly. Simplify this by putting the x and y dimensions into polar form, since circles are much easier to work with there. The net effect is that now we’re solving the problem in cylindrical coordinates -- height is still z, and positions in the horizontal dimensions are given in terms of angle and distance.

In order to cover all points within 1 unit of the cylinder’s axis, we’ll need all angles in a complete circle, and all radii between 0 and 1 (the radius of the cylinder). So Θ ranges from 0 to 2π, and r from 0 to 1:

Next, we need to express density in terms of the cylindrical coordinates r, Θ, and z instead of x, y, and z. To do that, recall the formulas for converting between rectangular and cylindrical coordinates, and look for places in the density function to apply them. The formula r² = x² + y² has immediate use...

The rest is just evaluating the iterated integral, i.e., evaluating each integral in turn from inner-most to outer-most:

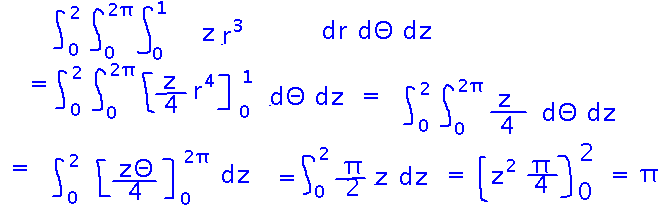
Work as a Line Integral

What sort of integral is it?

Because work is the component of force directed parallel to the direction of motion, times distance, it’s a circulation-style line integral (even though it’s not about circulation per se).

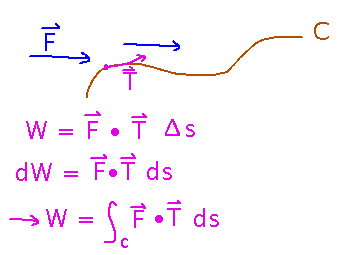
Vectors

Why does the sample exam question about finding the center of a rectangle from a corner and vectors along two sides add half of each vector to the corner?

Think in geometric terms of vector addition joining two vectors head-to-tail. Then notice that joining half of the vector along one side to half the vector along the other gets you to the center:

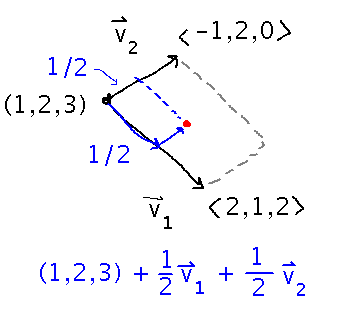
You can also think of this as going half way to the opposite corner. Mathematically, the two views give you the same answer.

Lagrange Multipliers

Find the point(s) on y = 2/x closest to the origin (sample exam problem).

To phrase this as an optimization problem, realize that it’s really asking you to minimize distance from the origin, subject to a constraint on y and x. Minimizing distance is equivalent to minimizing the square of the distance, so do that to simplify the later calculus a little.

The Lagrange multiplier strategy takes advantage of a relationship between the gradients of the objective function (f) and the constraint (g):

It’s almost always good to start using Lagrange multipliers by expanding the relationship between gradients into a system of equations:

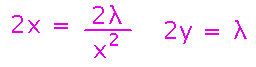
The system of equations isn’t necessarily a linear system, and it’s underconstrained (i.e., has more variables than equations), so what you do with it is a matter of problem-specific cleverness. In this case, rewriting both equations to express λ in terms of x and y gives us a way to express x in terms of y:

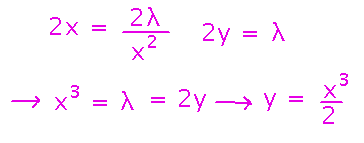
Finally, we can use this expression to rewrite the constraint in terms of a single variable and solve for that variable. Then finish by solving for the other:

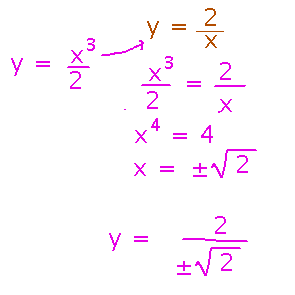
(Notice that the requirement that x ≠ 0 is important, because it rules out the “easy” solution of x = y = λ = 0 to the system of equations.)

(No Next Lecture)