Green’s Theorem on More General Regions

Return to Course Outline

Previous Lecture

Misc

Final

Friday, December 14, 8:00 AM

Comprehensive, but with emphasis on material since last hour exam (e.g., multiple integrals, line integrals, vector fields, Green’s Theorem, etc.)

Designed for 2 hours, you’ll have 3 1/3.

Rules and format otherwise similar to hour exams, especially open-references and calculator/computer rules.

I’ll put some sample questions on Canvas.

I’ll bring donuts and cider.

Review Session

11:30 - 12:30, Fraser 202A (our usual classroom), on study day.

SOFIs

6 responses. Thank you, but...

... please do submit more, they’re helpful to me.

Questions?

Problem Set Question 2

Use polar coordinates for integrating over the semicircle?

You can, although this particular problem might be simpler than that.

If you do use polar coordinates, the bounds would be 0 to π for Θ and 0 to 1 for r.

Problem Set Question 3

A good way to show that the field is conservative is to try to find its potential function. Do this by alternating integrations and differentiations, as we did for 2- and 3-dimensional fields.

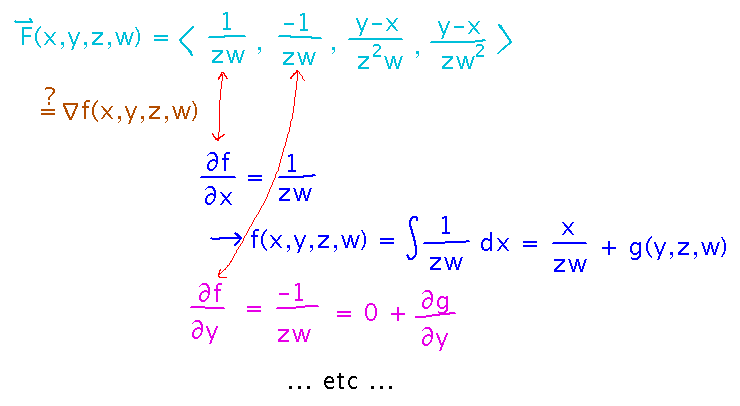
Green’s Theorem on Regions with Holes

“Green’s Theorem on General Regions” in section 6.4.

Theorem

What does the extension of Green’s Theorem say?

That with some care about how boundaries are oriented, you can use Green’s Theorem on regions with holes.

Example

Use Green’s Theorem to evaluate the circulation of F(x,y) = 〈 y, -x 〉 around the boundaries of a region consisting of a radius-2 circle centered at the origin, with the triangle with vertices (0,0), (1,0), and (0,1) removed:

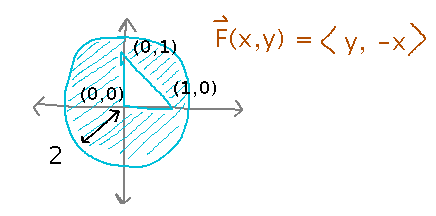
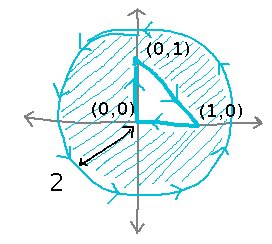
How do the boundaries have to be oriented in order to apply the extended Green’s Theorem?

The outer boundary needs to be traversed counterclockwise, the inner clockwise (keep the region of interest, aka the region over which Green’s Theorem will integrate, to your left as you traverse the boundaries).

What is the value of the integral?

Start with the basic equation you’ll use, then figure out what the parts of it are:

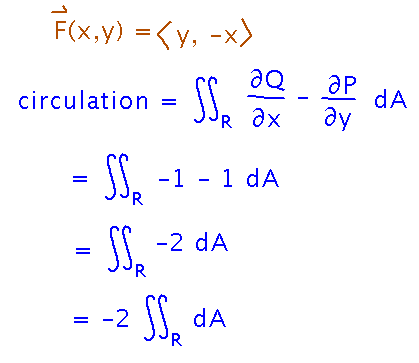
At this point we just have the area of the region times -2 -- we don’t even have to work out bounds for the integrals.

Key Points

Green’s Theorem changes very little for regions with holes

Next

Two other derivative-based operators on vector fields: divergence and curl.

Read section 6.5.

Next Lecture