Misc
Colloquium
Prof. Ahmad Almomani
“Bessel Integrals”
Today (December 5), 4:00 - 5:00 PM
Newton 203
Extra credit for short reactions, as usual.
Final
Friday, December 14, 8:00 AM
Comprehensive, but with emphasis on material since last hour exam (e.g., multiple integrals, line integrals, vector fields, Green’s Theorem, etc.)
Designed for 2 hours, you’ll have 3 1/3.
Rules and format otherwise similar to hour exams, especially open-references and calculator/computer rules.
I’ll put some sample questions on Canvas.
I’ll bring donuts and cider.
Review Session
11:30 - 12:30, Fraser 202A (our usual classroom), on study day.
SOFIs
Still 4 responses. Thank you, but...
... please do submit more, they’re helpful to me.
Questions?
More Green’s Theorem for Circulation
Example
Last time we got part way through an example: find the circulation of F(x,y) = ⟨ -xy2, x2y ⟩ counterclockwise around the trapezoid with vertices (0,0), (1,0), (1,2), (0,1).
Finish this, especially where the bounds come from and what the actual integral is.
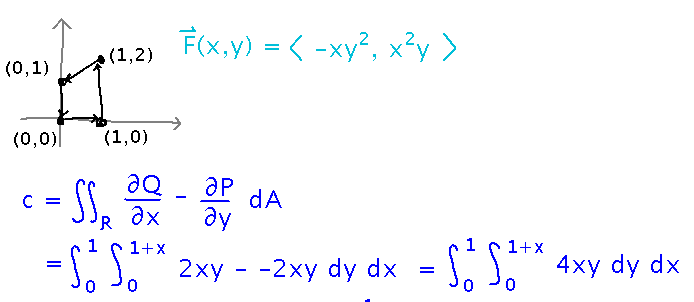
The bounds come from a typical analysis of bounds for a multivariable integral: consider the ranges of values x and y take on, and figure out how to express one variable in terms of the other. Here, x ranges from 0 to 1, and for each x value the equation of the line at the top of the trapezoid gives the maximum value for y (the minimum is always 0). That line has slope 1 and y intercept 1, so its equation is y = x + 1.
With the bounds known, we can evaluate the integral:
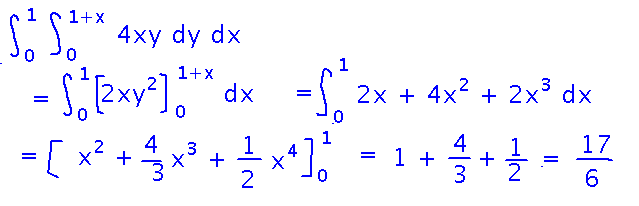
Area
You can also use Green’s Theorem in the opposite direction from what we’ve done so far, to convert an integral over some 2-dimensional region into a line integral. You saw an example when we discovered that certain line integrals evaluate to the area enclosed by the paths they integrate around.
To see how that works, notice that the field I gave you has derivatives for Green’s Theorem that produce an integrand of 1, i.e., an area integral:

More generally, if you can break the integrand in a 2-dimensional integral into a difference of pieces that can be viewed as the appropriate derivatives for Green’s Theorem, you can rephrase the integral as a line integral and evaluate it there.
Key Points
Using Green’s theorem to find a line integral in terms of a region integral.
The ability to convert from region integrals to line integrals, especially for area.
Green’s Theorem for Flux
Is there such a thing?
There is, as we can see by writing the general flux integral in differential form and then rearranging it to be evaluated via Green’s Theorem for circulation:
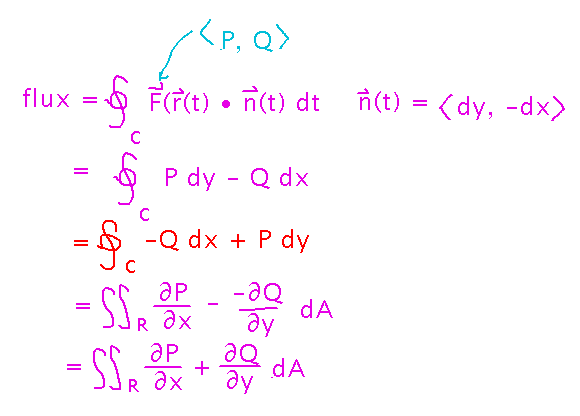
Another moral of this is that circulation and flux integrals aren’t really different, they’re just integrals of slightly different but related fields.
Next
Using the flux form of Green’s Theorem.
Read “Flux Form of Green’s Theorem” in section 6.4.