Misc
Colloquium
Prof. Ahmad Almomani
“Bessel Integrals”
Wednesday, December 5, 4:00 - 5:00 PM
Newton 203
Extra credit for short reactions, as usual.
Final
Friday, December 14, 8:00 AM
Comprehensive, but with emphasis on material since last hour exam (e.g., multiple integrals, line integrals, vector fields, Green’s Theorem, etc.)
Designed for 2 hours, you’ll have 3 1/3.
Rules and format otherwise similar to hour exams, especially open-references and calculator/computer rules.
I’ll put some sample questions on Canvas.
I’ll bring donuts and cider.
Review Session
11:30 - 12:30, Fraser 202A (our usual classroom), on study day.
SOFIs
4 responses (17%) now. Thank you!
But please do submit more responses, they’re helpful to me.
Questions?
How to start question 4 on problem set 12?
The question asks you to show that the sum of 2 conservative vector fields is conservative, and that any scalar multiple of a conservative vector field is conservative.
This is typical of lots of math questions that ask you to show that some property is “closed” under addition or scalar multiplication, i.e., that if 2 things have the property then their sum does too, or that if something has the property then so does any scalar multiple of that thing.
You can generally follow the same template for all such arguments: express the “things” in terms of the property in question, use algebra to rearrange the sum or product to show that they must be equal to something else with the property.
In this case, a good “property” to use is the fact that conservative vector fields are gradient fields, and vice versa. As soon as you can show that F + G is the gradient of some other function, you’ve shown that it’s conservative.
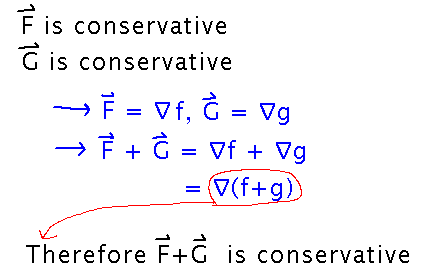
Green’s Theorem (Circulation Form)
“Circulation Form of Green’s Theorem” in section 6.4.
Line Integrals and Area
Did anyone spot a connection between areas and values of line integrals after Friday? (Find the circulation of 〈 -y/2, x/2 〉around circles of radius 1 and 2 centered at the origin.)
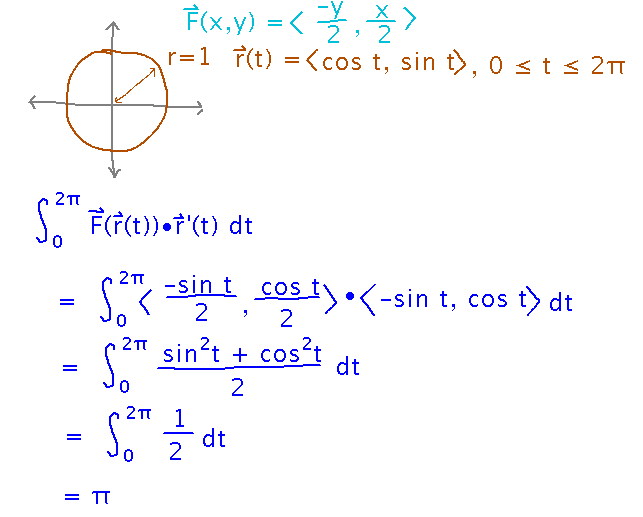
Oddly, the line integral has the same value as the area of the circle.
This particular field is purely circulatory, i.e., tangent to any radial vector coming from the origin.
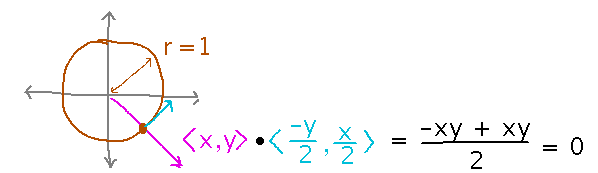
But this isn’t why the integral and the area are the same. In fact the same happens with other fields, for instance G(x,y) = 〈 y, 2x 〉, and happens when integrating around any closed curve, not just this circle.
What did that have to do with the reading? It’s a special case of Green’s Theorem!
Green’s Theorem says that there is a relationship between a line integral around a closed curve and a double integral over the region enclosed by that curve. By picking the right vector field, you can get that double integral to be the one that gives you area.
Green’s Theorem Example
Find the circulation of F(x,y) =〈 -xy2, x2y 〉around the trapezoid with vertices (0,0), (1,0), (1,2), (0,1), traversed counterclockwise.
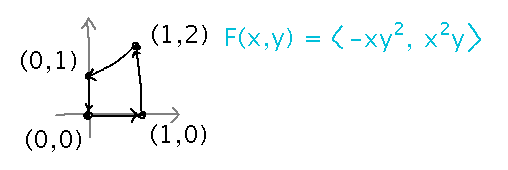
Rather than evaluating 4 separate line integrals, one for each side of the trapezoid, it’s easier to use Green’s Theorem and evaluate an integral over the trapezoid:
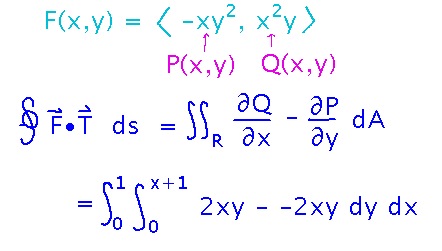
We have the integral set up, but will talk about the bounds and finish evaluating it Wednesday.
Key Points
Green’s Theorem relates line integrals of vector fields around closed paths to double integrals over the regions enclosed by the path.
Formula for circulation form of the theorem.
Next
More Green’s Theorem.
Start looking at the flux form.