Misc
SOFIs
Still 2 responses. Thank you!
But please do more — your feedback can make a difference in how I teach this or other courses in the future.
Review Session
Tuesday, December 11, 11:30 - 12:30, Fraser 202A (i.e., our regular time in our regular room).
Questions?
What is the book saying about a strategy for finding potential functions?
It comes down to an alternating process of integrations and differentiations, taking advantage of the fact that the vector field, F, is the gradient of the potential function, f (if there’s a potential function at all).
The first step is to integrate (an indefinite integral, find an antiderivative) the x component of the field with respect to x. Theoretically, that inverts the differentiation with respect to x that produces the first component of a gradient. But there’s a small problem, in that the constant of integration isn’t really a constant, it’s more a “function of integration,” h, that depends on all the variables in the problem except x.
So the second step is to differentiate the potential function from step 1 with respect to y. This produces an expression involving the derivative of h and some other terms. That expression should be equal to the 2nd component of the field (since the second component of a gradient is a derivative with respect to y); most likely some terms in the derivative will cancel against terms from the second component of F, leaving you with the derivative of h equaling the remaining terms.
Now step 3 is to integrate again, in order to learn what h (i.e., the part of the potential function that doesn’t depend on x) is. This will typically lead to another “function of integration” that now doesn’t depend on x or y, but does depend on other variables.
Do more differentiate-then-integrate cycles to eliminate variables 1 at a time from the “functions of integration” until you finally get down to truly a constant of integration.
See the examples below.
Potential Functions
“Conservative Vector Fields and Potential Functions” from section 6.3.
Example
Yesterday we realized that you could integrate components of a vector field to try to find a function that it’s the gradient of.
For example, by integrating the second component of F(x,y,z) = 〈 2xy - sin z, x2 + z, y - x cos z〉, we realized that any potential function, f(x,y,z), must be of the form f(x,y,z) = x2y + zy + g(x,z).
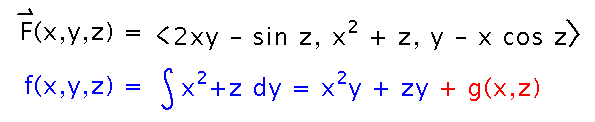
Where can we go from here? Do a differentiate-then-integrate cycle with respect to x (it could be any variable we haven’t already used, i.e., any variable but y at this point). Differentiate f with respect to x, and see what the need for that derivative to equal the first component of F implies about g’s derivative:
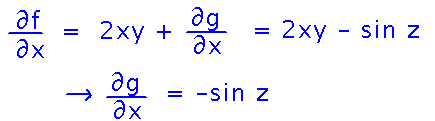
Now integrate g’s derivative to get a better estimate of f:
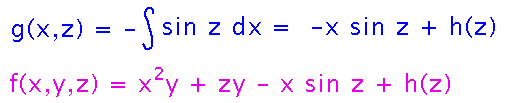
Finally, do diffferentiate-then-integrate one more time, with respect to z, to learn f up to just a constant of integration:
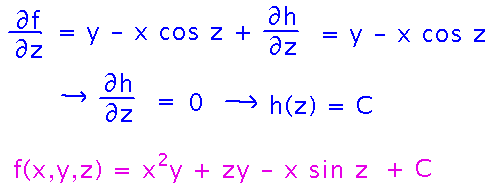
Try Your Own
What is the potential function for F(x,y) = 〈 1/(2√x) + yex, ex - 2y 〉?
Start by integrating with respect to y, then one differentiate-then-integrate cycle gives you the function:

What about a potential function for G(x,y,z) = 〈 yx2, z, yz2 〉? Start by integrating the y component of G, then differentiating with respect to x:
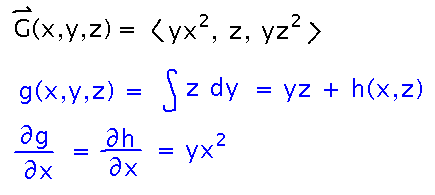
But here there’s a problem, because h is supposed to depend only on x and z, but even its derivative depends on y.
This is the kind of problem that comes up when the vector field actually isn’t conservative, which is pretty common. So be prepared to find that your field isn’t conservative. As long as you’re alert for problems like this, you can use the ability to find a potential function (or not) as a test of whether a vector field is conservative (or not).
Key Points
The process for finding a potential function.
What happens to that process when a vector field isn’t conservative.
Recognizing Conservative Fields
Is there another way to show that〈 yx2, z, yz2 〉isn’t conservative?
The “cross partial” property can be useful for showing that a field is not conservative:
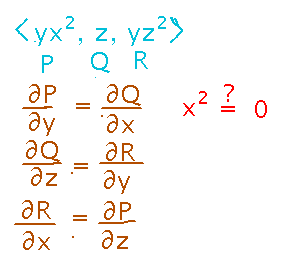
Key Point
The cross partial test.
Next
Consider F(x,y) = 〈 -y/2, x/2 〉. Find its circulation integral around circles of radius 1 and 2 centered at the origin. Then find the areas of those circles.
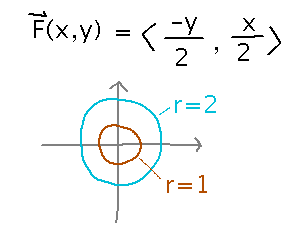
How come there’s a relation between the integrals and the areas? Green’s Theorem!
Read
- “Extending the Fundamental Theorem of Calculus”
- “Circulation Form of Green’s Theorem”
from section 6.4.