Misc
SOFIs
2 responses so far! Thank you!
Please do them — your feedback can make a difference in how I teach this or other courses in the future.
Review Session
Do you want one for around an hour on study day?
Yes.
Questions?
Conservative Vector Fields
Part of section 6.1, all of 6.3 (but we’ve only read the first half of 6.3 so far).
Example
Did anyone find a location or bag shape to give non-zero circulation around a bag of grains in the field F(x,y) = 〈 1, 1 〉?
〈 1, 1 〉= ∇(x+y), i.e., it’s conservative, i.e., any integral of it around a closed curve will equal 0.
Moral: conservative vector fields have lots of properties that can save you work, if you know that the field you’re dealing with is conservative.
Proof Practice
Can we clean up the proof of Theorem 6.1 (uniqueness of potential functions)?
If f and g are potential functions for F, then f = g + C
“Since f and g are both potential functions for F, then ∇ (f − g) = ∇ f − ∇g = F − F = 0. Let h = f − g, then we have ∇h = 0. We would like to show that h is a constant function.
“Assume h is a function of x and y (the logic of this proof extends to any number of independent variables). Since ∇h = 0, we have hx = 0 and hy = 0. The expression hx = 0 implies that h is a constant function with respect to x — that is, h(x, y) = k(y) for some function k. Similarly, hy = 0 implies k(y) = C. Thus, h(x, y) = C for some constant C on the connected domain of F. Note that we really do need connectedness at this point; if the domain of F came in two separate pieces, then C could be a constant C1 on one piece but could be a different constant C2 on the other piece. Since f - g = h = C, we have that f = g + C, as desired.”
The Fundamental Theorem for Line Integrals
Integrate F • T ds where F(x,y,z) =〈 y cos(xy), x cos(xy) - z sin(yz), -y sin(yz) 〉and the path in question is r(t) =〈 π/2 et-1, t, et-1 - 1 〉as t ranges from t = 0 to t = 1.
By the way, F = ∇f where f(x,y,z) = sin(xy) + cos(yz)
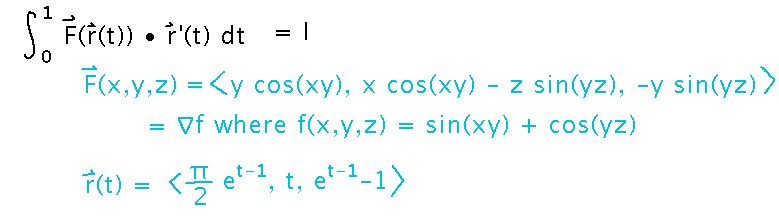
The fundamental theorem for line integrals gives us a much easier way to integrate this than the usual finding r′, taking the dot product, etc. Since F is a gradient, the thing it’s the gradient of (f) is the potential function, and you just need to evaluate f at the endpoints of the curve and subtract.
The endpoints of the curve are r(0) and r(1) here, so you do need to calculate those values.
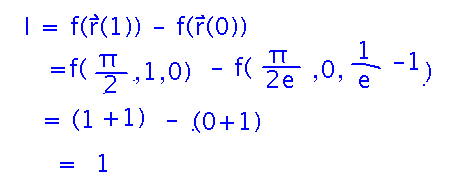
Key Points
The definition of gradient/conservative fields
The fundamental theorem and its application make evaluating integrals of conservative fields relatively easy.
Next
Finding potential functions is crucial to taking advantage of conservative fields, so how do you do that? For example, is this a conservative field?
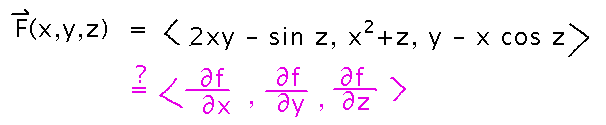
One way to find out is to try to find a potential function, which you can do by finding antiderivatives of the components of F. For example, starting with the simplest component of this example, we can integrate x2 + z with respect to y, since that term would have to be the partial derivative of any potential function with respect to y.
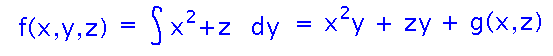
But there’s one trick to integrating multivariable functions: the “constants” of integration aren’t constants, they’re just functions that don’t depend on the variable you just integrated with respect to. Figuring out how to deal with that will be the starting point for tomorrow.
So between now and tomorrow, read
- “Conservative Vector Fields and Potential Functions”
- “Testing a Vector Field”
in section 6.3