Introduction to Vector Fields

Return to Course Outline

Previous Lecture

Questions?

Vector Fields

First 2 subsections of section 6.1.

2D Example

This is a vacuum tube, the key technology that enabled your grandparents to listen to the radio.

Internally, it sets up an electric field between a hot negatively charged filament and an outer positively charged shell. The flow of electrons from the negative filament to the positive shell can be modulated, providing a way to amplify the modulating signal.

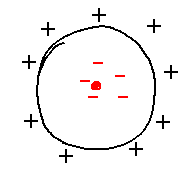
You can also think of this as a bottled vector field: the force that attracts electrons to the outer shell is a vector, and there is a force vector for each point in the tube.

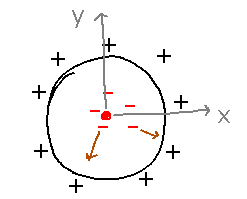
See if you can come up with a plausible electric field in a 2D cross section of a vacuum tube. Assume the force is a uniform 1 unit throughout the tube, and directed straight away from the origin. Vector 〈 x,y〉 has the right direction, but varies in magnitude. To get a vector in the same direction with constant magnitude 1, just divide by the original magnitude (i.e., make a unit vector):

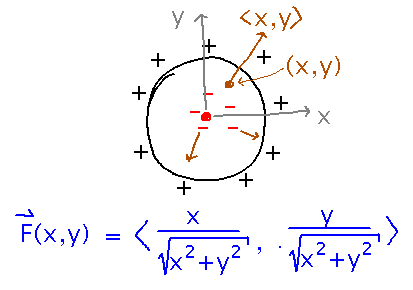
Plot It

Use VectorPlot or VectorPlot3D to plot vector fields in Mathematica.

Notebook “vectorfield.nb” contains a plot of the 2D vacuum tube field.

3D Example

Velocity in a whirlpool, i.e., rotational in the x and y directions with a slight downward component in z.

After some experimentation, we found 〈 y, -x, 0〉as a field that rotates around the z axis. To make the field point down with magnitude inversely related to z coordinate, consider using -1/z as the third component of the field, i.e., 〈 y, -x, -1/z 〉.

Mathematica notebook “vectorfield.nb” also shows a 3D plot of that vector field.

Key Points

Vector field = vector associated with each point in space or plane.

You’ve seen some building blocks for radial, rotational, constant-magnitude, etc. fields.

Plotting both 2D and 3D fields with Mathematica.

Next

Line integrals of vector fields.

Read “Vector Line Integrals” in section 6.2.

Next Lecture