Mass and Moments as Multiple Integrals

Return to Course Outline

Previous Lecture

Misc

History of Calculus Colloquium

Next Wednesday (November 14), 2:30, Newton 202.

Presented by Professors Johannes and Towsley.

Up to 2 points extra credit for attending and writing a paragraph on your reactions, connections to the ideas, etc. (but not just a summary of the content).

Questions?

Integration for Finding Masses and Moments

Section 5.6.

Definitions.

• Mass is related to weight (if you don’t have a more precise definition already, thinking of mass as being like weight will give you the right intuitions for our discussion).
• Moment (around a point, axis, or plane) is a measure of a mass’s tendency to make the thing it’s part of tip around that point/axis/plane. Calculated as mass times distance from the point/axis/plane.
• Center of Mass is the point at which opposing moments cancel out, so the object will balance if suspended from its center of mass.

Example

Indiana Jones and the Pyramid of Peril.

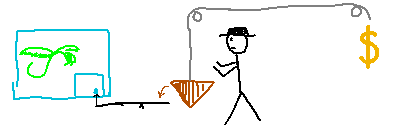
Indy could either tie the pyramid to another rope so that it doesn’t fall, but for better dramatic effect in the movies, he’ll carefully balance it so that the center of mass is exactly over the point.

Close-up of the pyramid (units are meters and kilograms):

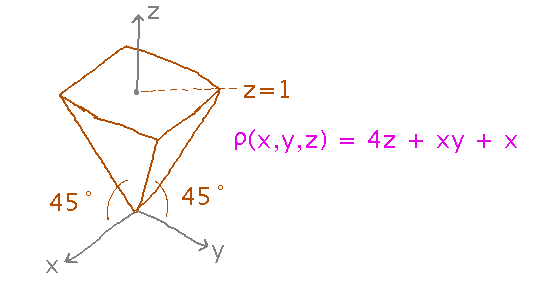
Where is the center of mass of the pyramid?

We have a lot of building blocks for answering this question in the textbook’s formulas. For example formulas for the coordinates of the center of mass in terms of moments and total mass.

We also have formulas for the mass and moments as integrals involving density.

Applying these integrals to our problem is mostly a matter of figuring out what the bounds should be. Figuring out the z bounds is easy (0 to 1). Then looking at a side view of the pyramid and asking how x (for example, y is identical) depends on z can give you expressions for the other bounds (-z to z).

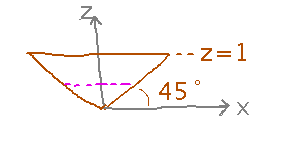
Using these bounds, we have an integral for mass:

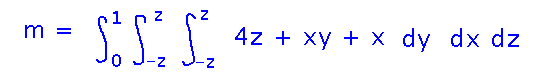
And a similar one, in particular with the same bounds, for moments:

Now use Mathematica to find the coordinates of the center of mass. Here’s a notebook that does it. Notice that it takes advantage of a feature you haven’t seen before, namely the ability to give a name to an expression that you’re going to use again. This can make it clearer what you’re doing in a Mathematica session, particularly in a case like this where you’re solving some multi-step problem.

Key Points

Equations for

• Mass
• Moments
• Center of mass

Naming results or expressions for reuse in Mathematica.

Next

Line integrals - integrating a function along a path through its arguments.

For example: what’s the area of the back wall of the greenhouse from Thursday?

Read “Scalar Line Integrals” in section 6.2.

Next Lecture