Multiple Integrals in Polar Coordinates

Return to Course Outline

Previous Lecture

Questions?

Problem Set Question 2

How to set up the Lagrange multiplier for this problem. Does it really lead to something as simple as x = y?

Sort of.

The first step is identifying the objective and constraint functions, and setting up the Lagrange multiplier equation:

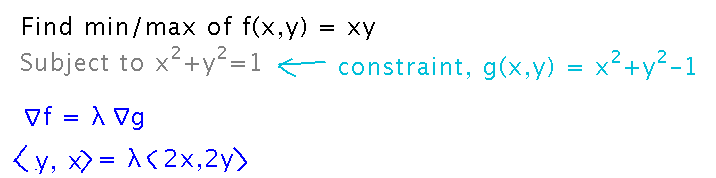
The resulting system of equations does indeed lead to a simple relationship between x and y, but beware of two things: first, in dividing by x and y you are assuming they aren’t 0. Effectively, you have “divided out” possible solutions in which they are. So make a note for yourself to come back and check separately whether those values do lead to minima/maxima.

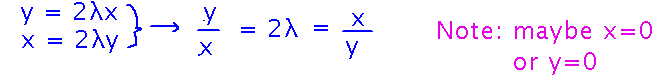
Second, the actual solution to x/y = y/x is x = y or x = -y, not just x = y.

Multiple Integrals in Mathematica

Idea: Integrate can take multiple x, y, etc. bounds. Give them in the order of the integrals they describe.

Here is an example illustrating a couple of uses.

Up to 2 points extra credit for checking Mathematica’s results by hand (or more accurately, checking that I used Mathematica right).

Double Integrals in Polar Form

Section 5.3.

Initial Example

What’s the volume between the circle x² + y² = 4 and the surface z = 4 - x² + y² ?

We could do this in rectangular coordinates, but the square roots coming from the circular region make the integrals harder to evaluate.

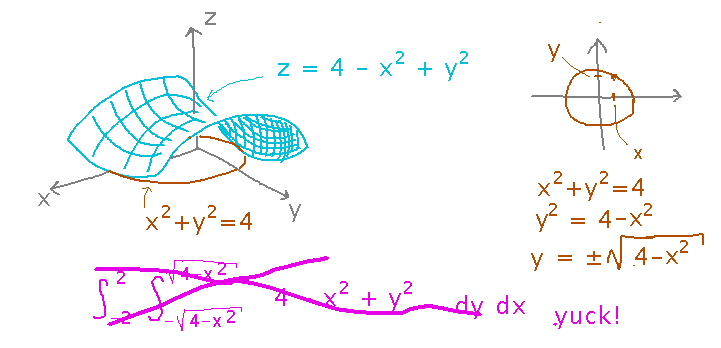
Polar coordinates provide a much nicer way to deal with circles, and can make integrals such as this much easier to evaluate. What do you get if you set up a polar coordinate integral up for this problem?

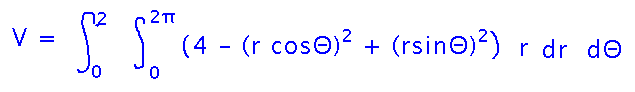
Key Points

Convert f(x,y) to g(r,Θ) using x = r cos Θ, y = r sinΘ, r² = x²+y², etc.

Express bounds in terms of r and Θ.

dx dy becomes r dr dΘ.

Next

Evaluate the integral from the above example, look at another.

Next Lecture