Tangents to Multivariable Functions

Return to Course Outline

Previous Lecture

Questions?

Tangent Planes

Section 4.4.

Tangents

Consider how the length of the diagonal of a rectangle depends on the width and height of that rectangle:

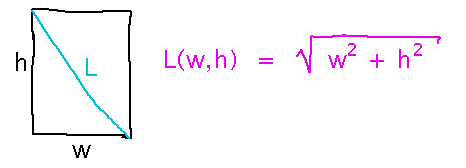
Then find an equation for the tangent plane to this function at (3,4). Use the textbook’s formula, with specific values from this problem filled in for the derivatives and reference point:

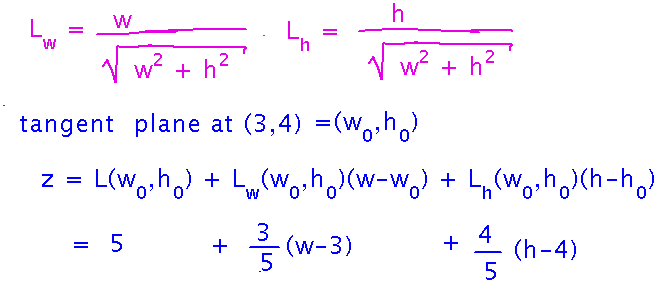
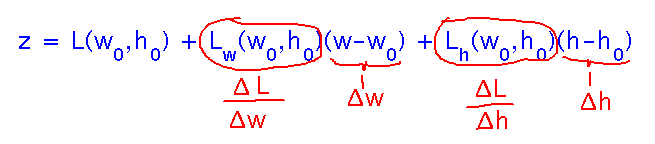
The rationale for the formula is that partial derivatives are rates of change with w and h, so multiplying them by the amount of change in w and h and adding to the function’s value at the reference point gives values along the tangent plane.

Linearization

Use a linear approximation to estimate the length of the diagonal if w = 2.9 and h = 4.05. Just use the tangent plane equation, with these w and h values:

Key Points

The equation for a tangent plane and the intuition behind it.

Using tangent planes to...

• Estimate the value of the function
• Define “differentiability” of multivariable functions (see textbook).

Next

The chain rule for multivariable functions.

Read section 4.5.

Guiding problem: Suppose z = f(x,y), x = g(s,t,u), and y = h(s). Find the partial derivatives of z with respect to s, t, and u, and draw the corresponding tree diagram.

Next Lecture