SUNY Geneseo Department of Mathematics

Integrals of Vector Valued Functions

Wednesday, September 26

Math 223 01
Fall 2018
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Questions?

Exponentials in Mathematica?

Use the Exp function.

See an example in today’s Mathematica notebook (which otherwise demonstrates vector integrals).

Antiderivatives and Integrals of Vector Valued Functions

Last part of section 3.2.

Idea

Suppose r(t) = 〈 3t2-1,1/t, 2/(2t+1), 1/(1+t2) 〉. Find the most general antiderivative of r.

The key idea is that an integral (definite or indefinite) of a vector valued function is the vector of integrals of the component functions.

These component functions illustrate some standard integrals, and one opportunity to practice u-substitution.

Also notice how the constant of integration can be written as a constant vector.

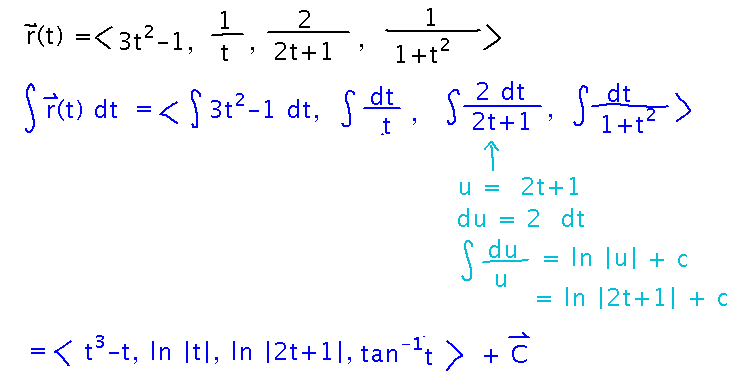
Integrate components of a vector using power rule, substitution, derivatives of ln and arctan

Suppose f(t) = 〈 cos t, sin t, t/π 〉. Find the integral of f between 0 and π/2.

Here too the key thing is to integrate each of the component functions.

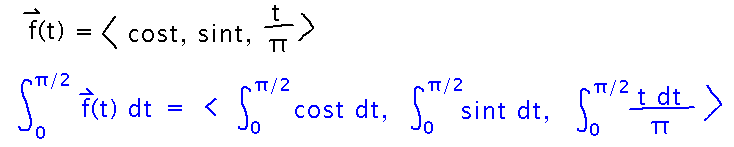
Definite integral of a vector is a vector of definite integrals of components

Once that’s done though, you can evaluate the whole vector at the bounds and describe the resulting calculation in terms of vector subtraction:

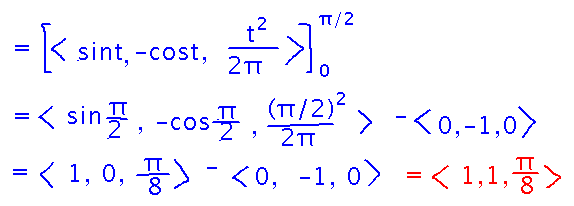
Evaluate vector at upper and lower t values and subtract

Acceleration / Velocity / Position

I once saw a fly try to fly over a charcoal grill. Sadly the heat killed the fly in mid-flight, leading it to fall in a perfectly parabolic path from above the grill to the ground. Find an equation for that path if the fly dies at point (0,0,3), while moving with velocity 〈 1, -1, 0 〉.

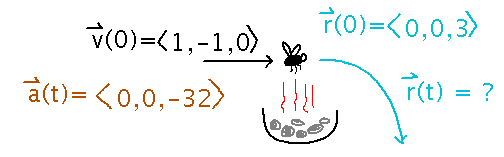
Fly flying above grill and then dropping

Since acceleration is the derivative of velocity, and velocity the derivative of position, you can integrate acceleration to get velocity, and then velocity to get position.

At each step, use the known values at t = 0 to find the constants of integration.

Calculate velocity first...

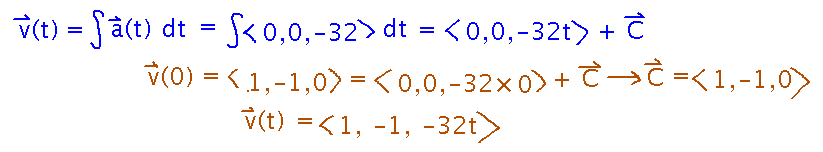
Integrate acceleration to get velocity, then evaluate at 0 and compare to v(0) to get constant

...and then position:

Integrate velocity and solve for constant to get position

Mathematica

The Integrate function integrates a function, including vectors.

Integrate[ ...some function of x... , x ] computes an indefinite integral with respect to x

Integrate[ ...some function of x..., {x, low, high} ] computes a definite integral between x = low and x = high.

For example, here is Mathematica calculating the two integrals from the “Idea” section above

Key Points

Calculate definite and indefinite integrals by integrating each component.

Application to acceleration/velocity/position.

Solving initial value problems.

Integration in Mathematica.

Next

Arc length of parametric curves

Read the

subsections of section 3.3.

Bring computers

Next Lecture