Derivatives of Vector Valued Functions

Misc

Extra credit colloquium write-ups are due any time before our final exam.

Questions?

Derivatives of Vector Valued Functions

First parts of section 3.2

Basic Idea

Find the derivative of 〈 1/t, tan(2t), √(sin t + cos t), e^t/(2t+1) 〉

The key idea is to differentiate each component of the vector. That plus a little chance to review differentiation produces...

Find the second derivative of 〈 s² - 3s + 1/s, sin(2s) 〉

Higher-order derivatives work exactly as you would expect, just take derivatives multiple times.

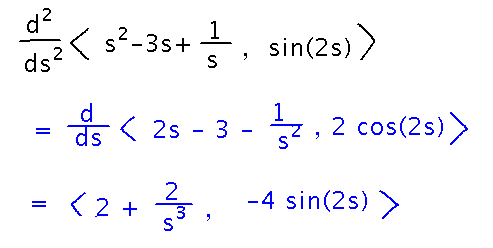
Applications

What’s the velocity of a particle moving along the path 〈 sin t, cos t, t 〉?

Velocity is the derivative of position

Find the unit tangent vector to that path

The derivative is also tangent to the curve at all points. The unit tangent vector is just the derivative scaled to have length 1.

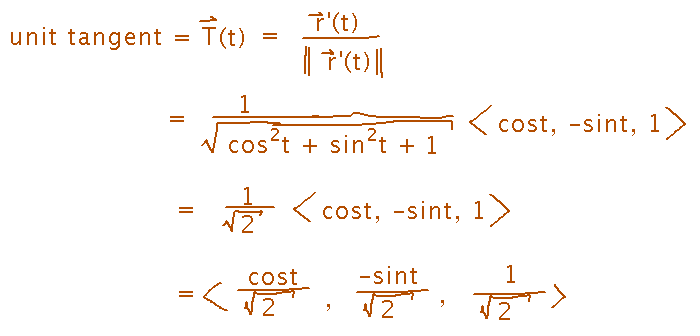
Proofs

Is that really a dot product in property vi of derivatives ( d/dt [r(f(t))] = r’(f(t)) • f’(t) )?

No, it has to be a scalar product just from the fact that the argument to r has to be a scalar.

You can also convince yourself of this by checking the derivation of that property:

Key Points

Differentiate a vector valued function by differentiating its components.

2nd derivatives work as expected.

Velocity, tangent, unit tangent vector.

Next

Integrals of vector valued functions.

Read the “Integrals of Vector-Valued Functions” subsection of section 3.2.