Limits of Vector Valued Functions

Return to Course Outline

Previous Lecture

Questions?

Limits of Vector Valued Functions

Formal Definition

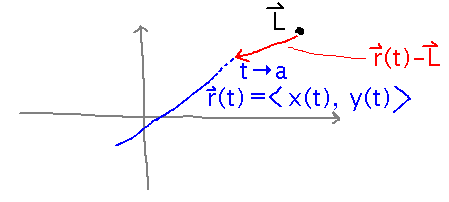
Draw a picture.

Start with the definition we’re trying to understand:

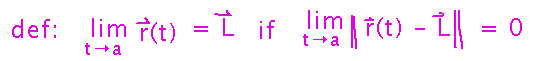
Think of the curve r(t) advancing through space as t approaches a. As it does so, the distance between L and the “tip” of the curve changes -- if the tip gets so close to L that the distance gets arbitrarily close to 0, it makes sense to say (and we do) that L is the limit of r.

Examples

Find lim_t→-2〈 ( t²-4)/(t+2), t²-4, (2t+4)/(3t+6) 〉

Use the idea that the limit of a vector function is the vector of limits of the individual component functions to turn this into a problem of finding lots of traditional scalar limits. You can use all the methods you know for finding such limits, for example L’Hôpital’s rule:

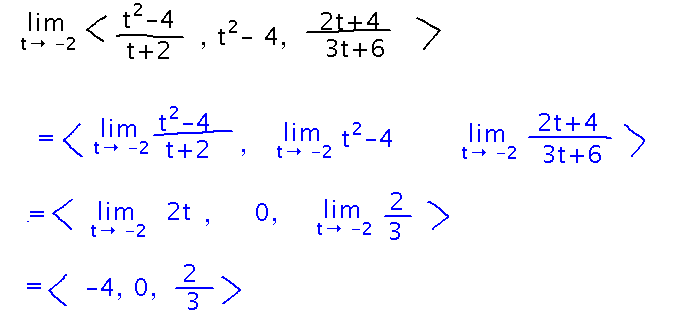
...or factoring, etc.

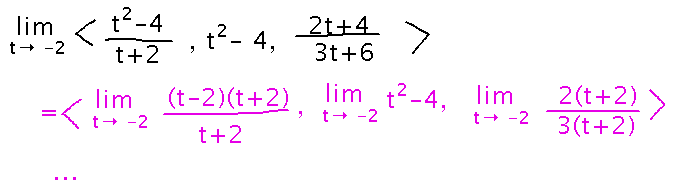
Find lim_t→0〈 1/t, 1, t 〉

This limit does not exist. Note that the whole vector limit doesn’t exist even though only one component fails to have a scalar limit.

Reasoning about Limits

Prove that if f(t) and g(t) are vector valued functions of the same dimension, c is a constant, and lim_t→cf(t) and lim_t→cg(t) exist, then lim_t→c (f(t)+g(t)) = lim_t→c f(t) + lim_t→c g(t).

The key idea is to think of the vectors in component form, then “push the limit inside the vector” where you can use familiar scalar limit laws.

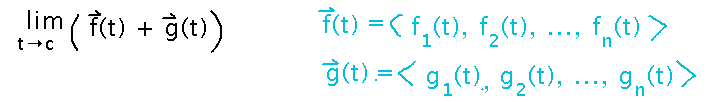
We’ll flesh this out tomorrow.

Key Points

The formal definition of a vector limit reflects an intuitively sensible idea.

The practical idea of a vector limit as a limit of vectors and how to work with it.

Problem Set

On vector valued functions and calculus with them.

See handout for details.

Next

Finish discussing limits of vector valued functions.

Bring computers to class, we’ll look at how to take limits with Mathematica.

Next Lecture