Questions?
Planes
Last two subsections of section 2.5.
Equations
Point and Perpendicular Line
Find an equation for the plane that contains (2,1,5) and is perpendicular to line r(t) = (1,2,3) + t〈2,-2,1〉
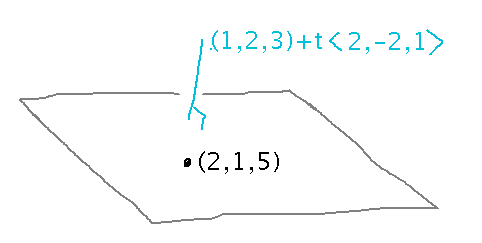
The key thing here is connections between the standard equation for a plane and the plane’s geometry, specifically that vector 〈A,B,C〉is the plane’s normal, and (x0,y0,z0) is any point on the plane. You can also rearrange the standard plane equation into other similar forms.
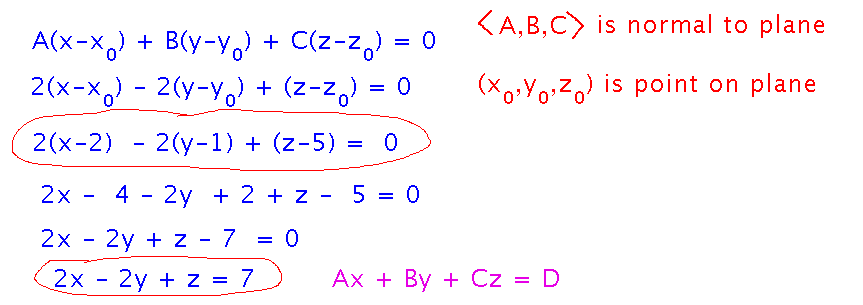
You can find points on a plane by setting 2 variables in the standard plane equation to “easy” values (e.g., 0) and then solving for the third. For example, this plane also contains point (0,0,7).
Two Lines
Find an equation for the plane that contains the lines r1(t) = (1,1,1) + t〈1,1,1〉and r2(t) = (1,1,1) + t〈1,0,-1〉.
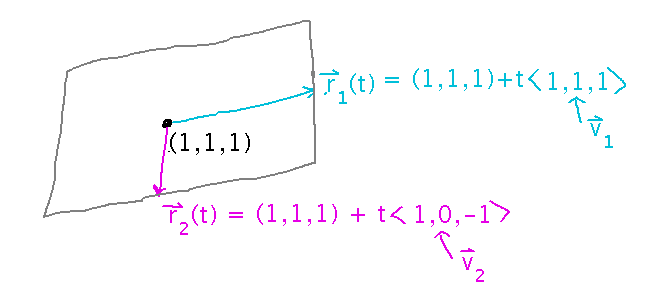
The key idea, which shows up in lots of calculations of planes’ equations, is that from two vectors parallel to a plane (like the direction vectors for these lines), the cross product will give you the normal. Then just plug any point on the plane in for x0, y0, and z0.
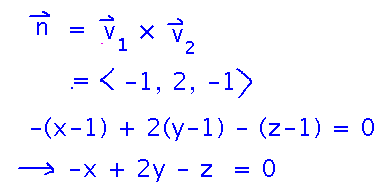
Distances
Consider plane x + y + z = 1
Which if any of these points lie in the plane, and which don’t?
- (1,0,0) Yes
- (2,1,2) No
Just plug x, y, and z into the plane equation and see if it holds or not
For those that don’t, how far are they from the plane?
Use the formula derived in the book, which basically realizes that any vector from the plane to the point in question extends for exactly the distance you want in the normal direction -- so the length of vector’s projection onto the normal is the desired distance.

Key Points
The standard equation for a plane and the geometric significance of its parts.
- You often use a cross product of vectors parallel to plane to find the normal.
The distance from a plane to a point.
Next
Vector valued functions.
Read the
- Definition of a Vector Valued Function
- Graphing Vector Valued Functions
subsections of section 3.1.