Misc
Programming and Data Science club has first meeting today -- 7:00 PM, Bailey 105. Snacks included!
Questions?
Trace?
What does the problem set mean by describing a paraboloid as having a “trace in the z = 1 plane” that’s a circle of radius 1?
A trace is a cross-section in a plane parallel to a set of axes. So in this case, if you take the plane z = 1, and ask how it intersects the paraboloid, the answer is that the intersection is a circle and has radius 1.

Cylindrical z?
Why do cylindrical coordinates include z?
Think of them as intermediate between a fully rectangular coordinate system and a fully circle-based one. They essentially use polar coordinates for 2 dimensions, but rectangular for the 3rd.
Cylindrical Coordinates
Cylindrical to Rectangular
What are the coordinates of the bottom of the “P” on a soup can if the position on the surface of the can is r = 1, Θ = 60º, z = 2?
Use textbook equations x = r cos Θ, y = r sin Θ, z = z
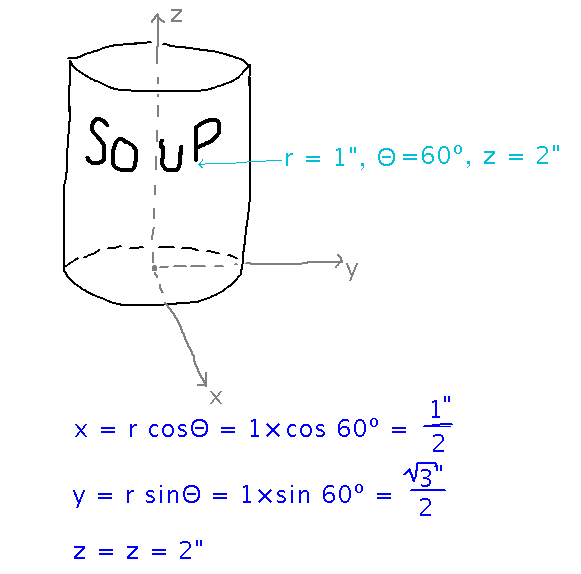
Note that the first 2 of these come from the fact that r and Θ are exactly like the r and Θ in polar coordinates and the definitions of sine and cosine in terms of sides of a triangle.
Rectangular to Cylindrical
What about point ( √2/2, -√2/2, 1.5 )? What are its coordinates relative to the can? Is it on the can, inside it, or outside?
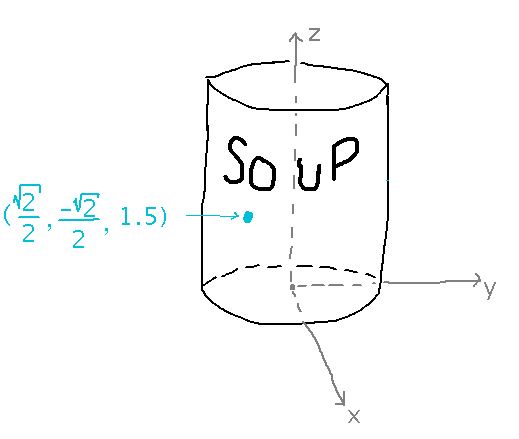
You can derive an equation for Θ by rearranging the equations for x and y:
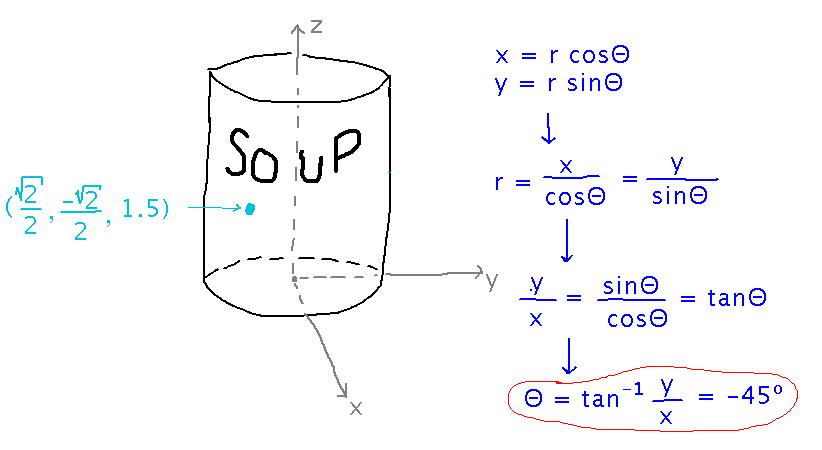
Beware in using this that around a full 360-degree circle, there will always be 2 angles whose tangent is y/x. You have to use the quadrant the point lies in to choose the correct angle. In this case the choices are -45 degrees (aka 315 degrees) and 135 degrees, but only -45 corresponds to a point in the 4th quadrant (i.e., with positive x and negative y).
Now you can substitute Θ back into the equation for x or y to find r:
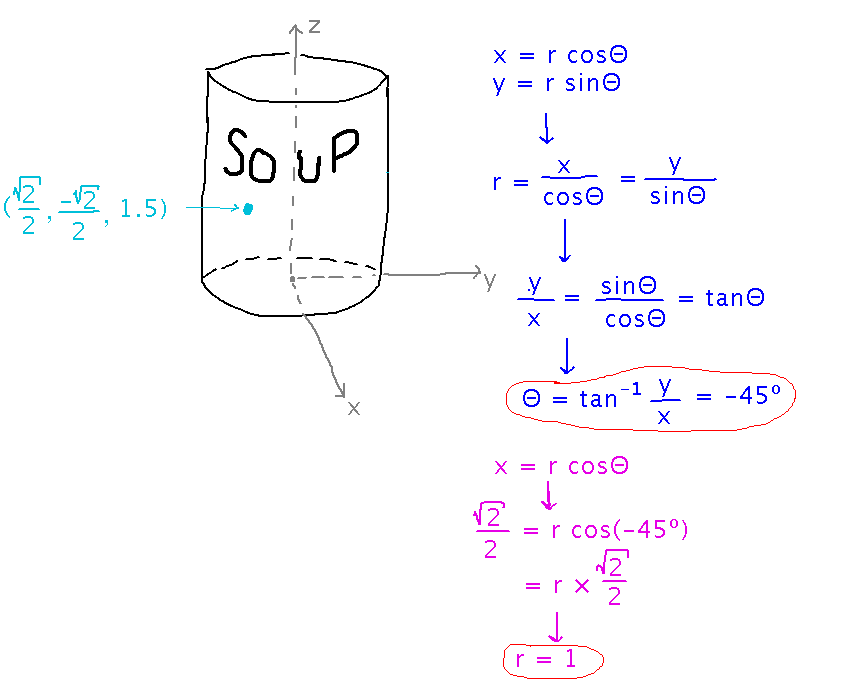
(You could also use the more-common-in-textbooks equation r = √(x2+y2), from the Pythagorean Theorem and since x and y are the lengths of the legs of a right triangle whose hypotenuse is r.)
And finally of course we have z = z = 1.5.
Assuming the same parameters for the can as in the first example, the fact that r equals the radius of the can and z is a value we know lies within the bounds of the can (since the can sits on the origin and has height at least 2), the point lies on the can.
Spherical Coordinates
Latitude & Longitude
Geneseo is at latitude 43º N and longitude 78º W. What are its coordinates in a right-handed rectangular coordinate system whose positive x axis comes out of the earth on the Prime Meridian at the equator, and whose positive z axis comes out of the earth at the North Pole?
Earth’s radius is approximately 4000 miles.
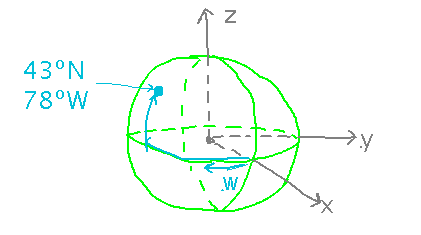
Start by converting latitude, measured up from the equator, to the book’s polar angle, measured down from the pole. Express longitude as an angle measured from the x axis towards the y while we’re at it:
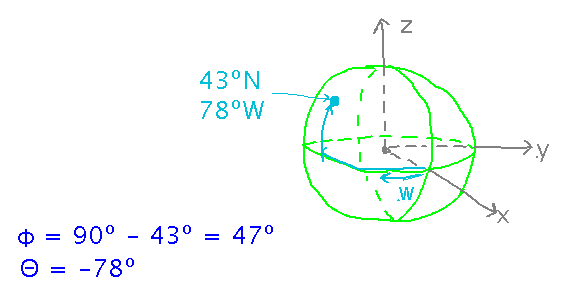
Now use textbook’s formulas (which again come from realizing that various radii lie on hypotenuses of right triangles whose legs are x, y, or z values):
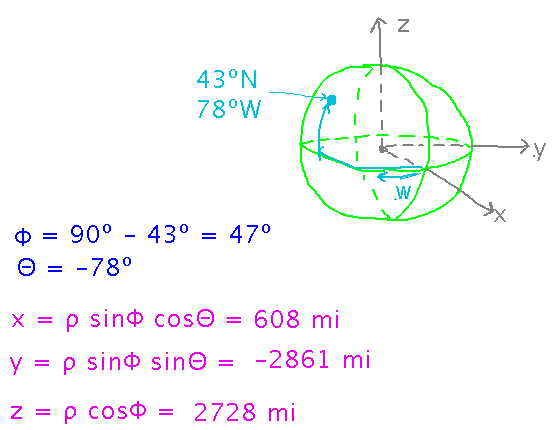
Key Points
That cylindrical and spherical coordinate systems exist
How they work
Conversions between them and rectangular
Next
Vectors
Read “Working with Vectors in R3” from section 2.2.